题目内容
【题目】已知![]() 、
、![]() 为椭圆
为椭圆![]() :
: ![]() (
(![]() )的左、右焦点,点
)的左、右焦点,点![]() 为椭圆上一点,且
为椭圆上一点,且![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若圆![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() :
: ![]() 与圆
与圆![]() 相切,并与椭圆
相切,并与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据椭圆定义得![]() ,再代入点P坐标得
,再代入点P坐标得![]() (2)由直线与圆相切得
(2)由直线与圆相切得![]() ,由
,由![]() ,利用向量数量积得
,利用向量数量积得![]() ,联立直线方程与椭圆方程,结合韦达定理代入化简得
,联立直线方程与椭圆方程,结合韦达定理代入化简得![]() 的值.
的值.
试题解析:(1)由题意得: 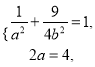 解得
解得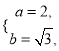
则椭圆方程为![]() .
.
(2)由直线![]() 与圆
与圆![]() 相切,得
相切,得![]() ,
, ![]() ,
,
设![]() ,
, ![]() ,
,
由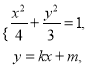 消去
消去![]() ,整理得
,整理得![]() ,
,
![]() 恒成立,
恒成立,
所以![]() ,
, ![]() ,
,
![]() ,
,
∵![]() ,
, ![]() ,
,
解得![]() .
.
点睛: 直线和圆锥曲线的位置关系,一般转化为直线方程与圆锥曲线方程组成的方程组,利用韦达定理或求根公式进行转化,涉及弦长的问题中,应熟练地利用根与系数关系,设而不求法计算弦长;涉及垂直关系时也往往利用根与系数关系、设而不求法简化运算;涉及过焦点的弦的问题,可考虑用圆锥曲线的定义求解.涉及中点弦问题往往利用点差法.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
【题目】近年来,某市实验中学校领导审时度势,深化教育教学改革,经过师生共同努力,高考成绩硕果累累,捷报频传,尤其是2017年某著名高校在全国范围内录取的大学生中就有25名来自该中学.下表为该中学近5年被录取到该著名高校的学生人数.(记2013年的年份序号为1,2014年的年份序号为2,依此类推……)
年份序号 | 1 | 2 | 3 | 4 | 5 |
录取人数 | 10 | 13 | 17 | 20 | 25 |
(1)求![]() 关于
关于![]() 的线性回归方程,并估计2018年该中学被该著名高校录取的学生人数(精确到整数);
的线性回归方程,并估计2018年该中学被该著名高校录取的学生人数(精确到整数);
(2)若在第1年和第4年录取的大学生中按分层抽样法抽取6人,再从这6人中任选2人,求这2人中恰好有一位来自第1年的概率.
参考数据:![]() ,
,![]() .
.
参考公式: ,
,![]() .
.