题目内容
【题目】如图,在三棱锥![]() 中,已知
中,已知![]() 是正三角形,平面
是正三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 在棱
在棱![]() 上,且
上,且![]() .
.
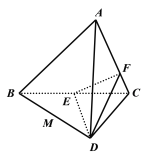
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,问
的中点,问![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,说明点
?若存在,说明点![]() 的位置;若不存在,试说明理由.
的位置;若不存在,试说明理由.
【答案】(1)证明见解析;(2)存在,![]() .
.
【解析】
(1)取![]() 中点
中点![]() ,由三角形中位线和已知长度关系可知
,由三角形中位线和已知长度关系可知![]() 且
且![]() 为
为![]() 中点,三线合一得到
中点,三线合一得到![]() ;由面面垂直性质可得
;由面面垂直性质可得![]() 平面
平面![]() ,由线面垂直性质知
,由线面垂直性质知![]() ;由线面垂直的判定定理可证得结论;
;由线面垂直的判定定理可证得结论;
(2)假设存在满足题意的点![]() ,由线面平行的性质可知
,由线面平行的性质可知![]() ;根据重心的性质可得到比例关系
;根据重心的性质可得到比例关系![]() ,即
,即![]() ,从而可说明存在点
,从而可说明存在点![]() .
.
(1)取![]() 中点
中点![]() ,连接
,连接![]()

![]() 分别为
分别为![]() 中点
中点 ![]()
又![]() ,
,![]()
![]()
![]()
![]() ,即
,即![]() 为
为![]() 中点
中点 ![]()
![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 中点
中点 ![]()
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
(2)假设![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]()
连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]()
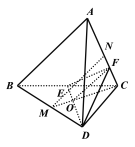
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]()
![]() 为等边
为等边![]() 的两条中线
的两条中线 ![]() 为
为![]() 的重心
的重心 ![]()
![]() ,即
,即![]()
![]()
![]() 存在点
存在点![]() ,满足
,满足![]() 时,
时,![]() 平面
平面![]()

练习册系列答案
相关题目
【题目】随着科技的发展,网购已经逐渐融入了人们的生活.在家里面不用出门就可以买到自己想要的东西,在网上付款即可,两三天就会送到自己的家门口,如果近的话当天买当天就能送到,或者第二天就能送到,所以网购是非常方便的购物方式.某公司组织统计了近五年来该公司网购的人数![]() (单位:人)与时间
(单位:人)与时间![]() (单位:年)的数据,列表如下:
(单位:年)的数据,列表如下:
| 1 | 2 | 3 | 4 | 5 |
| 24 | 27 | 41 | 64 | 79 |
(1)依据表中给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).(若
并加以说明(计算结果精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式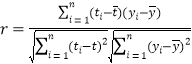
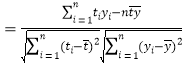 ,参考数据
,参考数据![]() .
.
(2)建立![]() 关于
关于![]() 的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
(参考公式: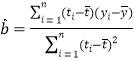
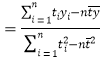 ,
,![]() )
)