题目内容
【题目】已知向量![]() ,向量
,向量![]() 是与向量
是与向量![]() 夹角为
夹角为![]() 的单位向量.
的单位向量.
(1)求向量![]() ;
;
(2)若向量![]() 与向量
与向量![]() 共线,且
共线,且![]() 与
与![]() 的夹角为钝角,求实数x的取值范围.
的夹角为钝角,求实数x的取值范围.
【答案】(1)![]() (0,1)或
(0,1)或 ;(2) (﹣∞,﹣2)∪(﹣2,
;(2) (﹣∞,﹣2)∪(﹣2,![]() )∪(0,2).
)∪(0,2).
【解析】
(1)设向量![]() ,由题意可得
,由题意可得 ,解方程组即可。
,解方程组即可。
(2)由(1)和向量![]() 与向量
与向量![]() 共线,可知
共线,可知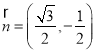 ,因为
,因为![]() 与
与![]() 的夹角为钝角,所以
的夹角为钝角,所以![]() ,且两个向量不共线,即可解出
,且两个向量不共线,即可解出![]() 的范围。
的范围。
(1)向量![]() ,向量
,向量![]() 是与向量
是与向量![]() 夹角为
夹角为![]() 的单位向量,
的单位向量,
则![]() (
(![]() ,
,![]() )=(cos
)=(cos![]() ,sin
,sin![]() ),
),
所以![]() (cos(
(cos(![]() ),sin(
),sin(![]() ))=(cos
))=(cos![]() ,sin
,sin![]() )=(0,1);
)=(0,1);
或![]() (cos(
(cos(![]() ),sin(
),sin(![]() ))=(cos
))=(cos![]() ,sin
,sin![]() )=(
)=(![]() ,
,![]() );
);
所以向量![]() (0,1)或
(0,1)或 ;
;
(2)由向量![]() 与向量
与向量![]() 共线,得
共线,得![]() (
(![]() ,
,![]() );
);
又![]() 与
与![]() 的夹角为钝角,
的夹角为钝角,
则![]() ,
,
即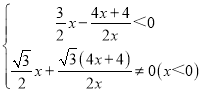 ,
,
解得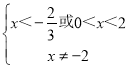 ,
,
所以实数x的取值范围是(﹣∞,﹣2)∪(﹣2,![]() )∪(0,2).
)∪(0,2).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】如图,设![]() 是由
是由![]()
![]() 个实数组成的
个实数组成的![]() 行
行![]() 列的数表,其中
列的数表,其中![]()
![]() 表示位于第
表示位于第![]() 行第
行第![]() 列的实数,且
列的实数,且![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
定义![]()
![]() 为第s行与第t行的积. 若对于任意
为第s行与第t行的积. 若对于任意![]() (
(![]() ),都有
),都有![]() ,则称数表
,则称数表![]() 为完美数表.
为完美数表.
(Ⅰ)当![]() 时,试写出一个符合条件的完美数表;
时,试写出一个符合条件的完美数表;
(Ⅱ)证明:不存在10行10列的完美数表;
(Ⅲ)设![]() 为
为![]() 行
行![]() 列的完美数表,且对于任意的
列的完美数表,且对于任意的![]() 和
和![]() ,都有
,都有![]() ,证明:
,证明:![]() .
.