题目内容
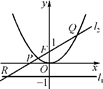
已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.
(1)求动点C的轨迹方程;
(2)过点F的直线l2交轨迹于两点P、Q,交直线l1于点R,求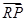 ·
·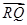 的最小值.
的最小值.
(1)求动点C的轨迹方程;
(2)过点F的直线l2交轨迹于两点P、Q,交直线l1于点R,求
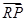 ·
·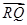 的最小值.
的最小值.(1)x2=4y(2)16
(1)由题设点C到点F的距离等于它到l1的距离,
∴点C的轨迹是以F为焦点,l1为准线的抛物线.∴所求轨迹的方程为x2=4y.
(2)由题意直线l2的方程为y=kx+1,与抛物线方程联立消去y,得x2-4kx-4=0.
记P(x1,y1),Q(x2,y2),则x1+x2=4k,x1x2=-4.
由直线PQ的斜率k≠0,易得点R的坐标为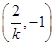 ,
,
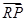 ·
·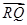 =
=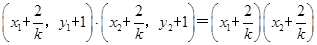 +(kx1+2)(kx2+2)
+(kx1+2)(kx2+2)
=(1+k2)x1x2+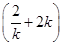 (x1+x2)+
(x1+x2)+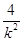 +4
+4
=-4(1+k2)+4k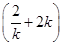 +
+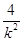 +4=4
+4=4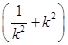 +8.
+8.
∵k2+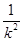 ≥2,当且仅当k2=1时取到等号.
≥2,当且仅当k2=1时取到等号.
∴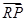 ·
·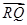 ≥4×2+8=16,即
≥4×2+8=16,即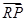 ·
·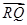 的最小值为16.
的最小值为16.
∴点C的轨迹是以F为焦点,l1为准线的抛物线.∴所求轨迹的方程为x2=4y.

(2)由题意直线l2的方程为y=kx+1,与抛物线方程联立消去y,得x2-4kx-4=0.
记P(x1,y1),Q(x2,y2),则x1+x2=4k,x1x2=-4.
由直线PQ的斜率k≠0,易得点R的坐标为
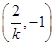 ,
,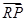 ·
·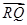 =
=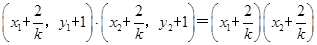 +(kx1+2)(kx2+2)
+(kx1+2)(kx2+2)=(1+k2)x1x2+
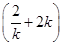 (x1+x2)+
(x1+x2)+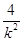 +4
+4=-4(1+k2)+4k
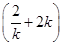 +
+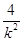 +4=4
+4=4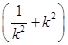 +8.
+8.∵k2+
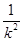 ≥2,当且仅当k2=1时取到等号.
≥2,当且仅当k2=1时取到等号.∴
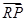 ·
·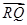 ≥4×2+8=16,即
≥4×2+8=16,即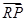 ·
·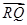 的最小值为16.
的最小值为16.
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
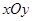 中,已知定点F(1,0),点
中,已知定点F(1,0),点 在
在 轴上运动,点
轴上运动,点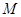 在
在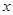 轴上,点
轴上,点
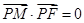 ,
,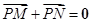 .
.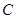 的方程;
的方程;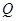 是直线
是直线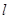 :
: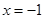 上任意一点,过点
上任意一点,过点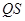 ,
,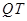 ,切点分别为
,切点分别为 ,
,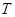 ,设切线
,设切线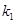 ,
,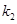 ,直线
,直线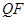 的斜率为
的斜率为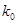 ,求证:
,求证: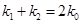 .
.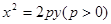 的焦点为
的焦点为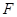 ,点
,点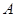 为抛物线上的一点,其纵坐标为
为抛物线上的一点,其纵坐标为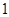 ,
,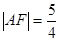 .
.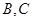 为抛物线上不同于
为抛物线上不同于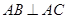 ,过
,过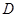 ,求
,求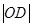 的最小值.
的最小值.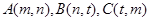 ,直线AC的斜率与倾斜角为钝角的直线AB的斜率之和为
,直线AC的斜率与倾斜角为钝角的直线AB的斜率之和为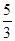 ,而直线AB恰好经过抛物线
,而直线AB恰好经过抛物线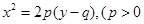 )的焦点F并且与抛物线交于P、Q两点(P在Y轴左侧).则
)的焦点F并且与抛物线交于P、Q两点(P在Y轴左侧).则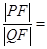 ( )
( )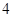
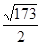

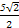 +2
+2