题目内容
11.掷两颗均匀的骰子,向上的点数之和为5的概率等于( )| A. | $\frac{1}{18}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{36}$ | D. | $\frac{1}{9}$ |
分析 本题是一个求概率的问题,考查事件“抛掷两颗骰子,所得两颗骰子的点数之和为5”这是一个古典概率模型,求出所有的基本事件数N与事件“抛掷两颗骰子,所得两颗骰子的点数之和为5”包含的基本事件数n,再由公式$\frac{n}{N}$求出概率得到
解答 解:抛掷两颗骰子所出现的不同结果数是6×6=36
事件“抛掷两颗骰子,所得两颗骰子的点数之和为5”所包含的基本事件有(1,4),(2,3),(3,2),(4,1)共四种
故事件“抛掷两颗骰子,所得两颗骰子的点数之和为5”的概率是$\frac{4}{36}$=$\frac{1}{9}$,
故选:D.
点评 本题是一个古典概率模型问题,解题的关键是理解事件“抛掷两颗骰子,所得两颗骰子的点数之和为5”,由列举法计算出事件所包含的基本事件数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.若角α和β的终边关于y轴对称,则下列各式中正确的是( )
| A. | sinα=sinβ | B. | cosα=cosβ | C. | tanα=tanβ | D. | cos(2π-α)=cosβ |
20.已知过点A(-2,m)和点B(m2,-7)的直线与直线y-1=-2(x+3)平行,则m的值为( )
| A. | $\frac{3}{2}$ | B. | -1 | C. | -1或$\frac{3}{2}$ | D. | 1或-1 |
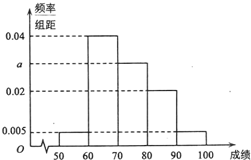 某校100名学生期末考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期末考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]. 的等边三角形
的等边三角形 的中线
的中线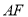 与中位线
与中位线 交于点
交于点 ,已知
,已知 是
是 绕
绕 旋转过程中的一个图形,则下列命题中正确的是( )
旋转过程中的一个图形,则下列命题中正确的是( )
 ;②
;② 平面
平面 ;③三棱锥
;③三棱锥 的体积有最大值.
的体积有最大值.