题目内容
20.已知过点A(-2,m)和点B(m2,-7)的直线与直线y-1=-2(x+3)平行,则m的值为( )| A. | $\frac{3}{2}$ | B. | -1 | C. | -1或$\frac{3}{2}$ | D. | 1或-1 |
分析 因为过点A(-2,m)和点B(m2,-7)的直线与直线y-1=-2(x+3)平行,所以两直线的斜率相等.
解答 解:∵直线y-1=-2(x+3)斜率等于-2,
∴过点A(-2,m)和B(m,4)的直线的斜k也是-2,
∴$\frac{-7-m}{{m}^{2}+2}$=-2,
解得m=-1或m=$\frac{3}{2}$,
当m=-1时,两直线重合故舍去,
故选:A.
点评 本题考查两斜率存在的直线平行的条件是斜率相等,以及斜率公式的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在实数范围内,下列不等关系不恒成立的是( )
| A. | x2≥0 | B. | a2+b2≥2ab | C. | x+1>x | D. | |x+1|>|x| |
11.掷两颗均匀的骰子,向上的点数之和为5的概率等于( )
| A. | $\frac{1}{18}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{36}$ | D. | $\frac{1}{9}$ |
15.在数列{an}中,已知对于n∈N*,有a1+a2+a3+…+an=2n-1,则a${\;}_{1}^{2}$+a${\;}_{2}^{2}$+…+a${\;}_{n}^{2}$=( )
| A. | 4n-1 | B. | $\frac{1}{3}$(4n-1) | C. | $\frac{1}{3}$(2n-1) | D. | (2n-1)2 |
11.设数列{an}中,已知a1=1,an=$\frac{1}{2{a}_{n-1}}$(n>1),则a2=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 2 |
 的定义域为( )
的定义域为( ) B.
B.
 D.
D.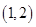
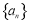 中,
中, ,
, ,则
,则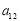 的值是( )
的值是( )