题目内容
11.设a、b、c∈R+,求证:$\frac{{a}^{2}}{a+b}$+$\frac{{b}^{2}}{b+c}$+$\frac{{c}^{2}}{c+a}$≥$\frac{a+b+c}{2}$.分析 由(a+b+b+c+c+a)($\frac{{a}^{2}}{a+b}$+$\frac{{b}^{2}}{b+c}$+$\frac{{c}^{2}}{c+a}$),展开后,由基本不等式,化简整理,即可得证.
解答 证明:由a、b、c∈R+,
由((a+b)+(b+c)+(c+a))($\frac{{a}^{2}}{a+b}$+$\frac{{b}^{2}}{b+c}$+$\frac{{c}^{2}}{c+a}$)
=a2+b2+c2+($\frac{(a+b)•{b}^{2}}{b+c}$+$\frac{(b+c)•{a}^{2}}{a+b}$)+($\frac{(a+b)•{c}^{2}}{c+a}$+$\frac{(c+a)•{a}^{2}}{a+b}$)+($\frac{(b+c)•{c}^{2}}{c+a}$+$\frac{(c+a)•{b}^{2}}{b+c}$)
≥a2+b2+c2+2ab+2ac+2bc=(a+b+c)2,
当且仅当a=b=c时,取得等号.
即有$\frac{{a}^{2}}{a+b}$+$\frac{{b}^{2}}{b+c}$+$\frac{{c}^{2}}{c+a}$≥$\frac{a+b+c}{2}$.
点评 本题考查不等式的证明,考查基本不等式的运用,考查化简整理能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

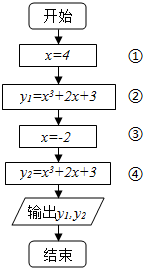 阅读如图所示的程序框图,回答下面的问题:
阅读如图所示的程序框图,回答下面的问题: