题目内容
(本小题满分13分)
已知函数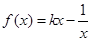 ,且
,且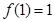 .(1)求实数k的值及函数的定义域;(2)判断函数在(0,+∞)上的单调性
.(1)求实数k的值及函数的定义域;(2)判断函数在(0,+∞)上的单调性
已知函数
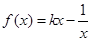 ,且
,且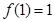 .(1)求实数k的值及函数的定义域;(2)判断函数在(0,+∞)上的单调性
.(1)求实数k的值及函数的定义域;(2)判断函数在(0,+∞)上的单调性解:(1)由f(1)=1得k=2,定义域为{x∈R|x≠0};…………………………………6分
(2)为增函数.在(0,+∞)任取两数x1,x2.设x2>x1>0,则f(x2)-f(x1)=(2x2-
 )-(2x1-
)-(2x1- )=(x2-x1)(2+
)=(x2-x1)(2+ )因为x2>x1>0,所以x2-x1>0,2+
)因为x2>x1>0,所以x2-x1>0,2+ >0,所以f(x2)-f(x1)>0,即f(x2)>f(x1),所以f(x)为增函数.…………………………………13分
>0,所以f(x2)-f(x1)>0,即f(x2)>f(x1),所以f(x)为增函数.…………………………………13分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,且当
,且当 时,
时, ,则
,则 =( )
=( )

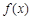 的定义域为
的定义域为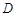 ,若存在非零实数
,若存在非零实数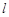 使得对于任意
使得对于任意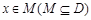 ,有
,有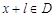 ,且
,且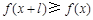 ,则称
,则称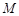 上的
上的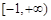 的函数
的函数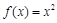 为
为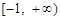 上的
上的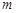 高调函数,那么实数
高调函数,那么实数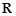 的函数
的函数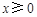 时,
时,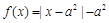 ,且
,且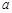 的取值范围是 .
的取值范围是 . 满足
满足 ,当
,当 时,
时,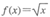 .又
.又 ,则集合
,则集合 等于
等于


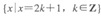
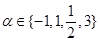 ,则使函数
,则使函数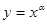 的定义域为
的定义域为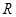 且为奇函数的所有
且为奇函数的所有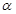 的值为
的值为 
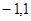


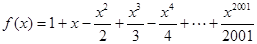 ,则函数f(x)在其定义域内的零点个数是( )
,则函数f(x)在其定义域内的零点个数是( ) 满足
满足 且
且 ,则
,则 等于 ( )
等于 ( )



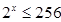 且
且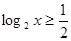 ,
,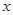 的取值范围;
的取值范围;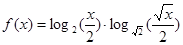 的最大值和最小值。
的最大值和最小值。 等于( )
等于( )


