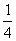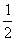题目内容
设函数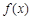 的定义域为
的定义域为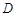 ,若存在非零实数
,若存在非零实数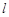 使得对于任意
使得对于任意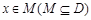 ,有
,有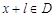 ,且
,且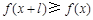 ,则称
,则称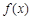 为
为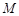 上的
上的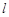 高调函数.如果定义域为
高调函数.如果定义域为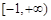 的函数
的函数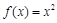 为
为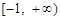 上的
上的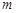 高调函数,那么实数
高调函数,那么实数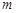 的取值范围是 .如果定义域为
的取值范围是 .如果定义域为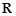 的函数
的函数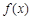 是奇函数,当
是奇函数,当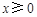 时,
时,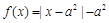 ,且
,且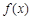 为
为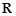 上的4高调函数,那么实数
上的4高调函数,那么实数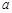 的取值范围是 .
的取值范围是 .
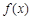 的定义域为
的定义域为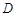 ,若存在非零实数
,若存在非零实数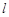 使得对于任意
使得对于任意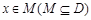 ,有
,有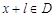 ,且
,且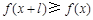 ,则称
,则称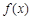 为
为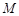 上的
上的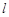 高调函数.如果定义域为
高调函数.如果定义域为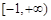 的函数
的函数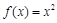 为
为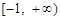 上的
上的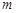 高调函数,那么实数
高调函数,那么实数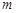 的取值范围是 .如果定义域为
的取值范围是 .如果定义域为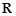 的函数
的函数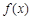 是奇函数,当
是奇函数,当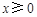 时,
时,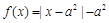 ,且
,且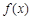 为
为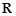 上的4高调函数,那么实数
上的4高调函数,那么实数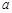 的取值范围是 .
的取值范围是 . ,
,
依题意可得, 且
且 对任意
对任意 都成立,即
都成立,即 对任意
对任意 都成立。因为
都成立。因为 ,所以有
,所以有 对任意
对任意 都成立,所以
都成立,所以 ,解得
,解得 。
。
依题意可得, 在R上恒成立。当
在R上恒成立。当 时,
时, 单调递增;当
单调递增;当 时,
时, 单调递减
单调递减
因为 为奇函数,所以当
为奇函数,所以当 时,
时, 。则当
。则当 时,
时, 单调递增;当
单调递增;当 时,
时, 单调递减
单调递减
综上可得, 当
当 或
或 时单调递增,当
时单调递增,当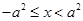 时单调递减,则其函数图象大致如下:
时单调递减,则其函数图象大致如下:

要使得 恒成立,则
恒成立,则 ,解得
,解得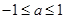
 且
且 对任意
对任意 都成立,即
都成立,即 对任意
对任意 都成立。因为
都成立。因为 ,所以有
,所以有 对任意
对任意 都成立,所以
都成立,所以 ,解得
,解得 。
。依题意可得,
 在R上恒成立。当
在R上恒成立。当 时,
时, 单调递增;当
单调递增;当 时,
时, 单调递减
单调递减因为
 为奇函数,所以当
为奇函数,所以当 时,
时, 。则当
。则当 时,
时, 单调递增;当
单调递增;当 时,
时, 单调递减
单调递减综上可得,
 当
当 或
或 时单调递增,当
时单调递增,当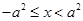 时单调递减,则其函数图象大致如下:
时单调递减,则其函数图象大致如下:
要使得
 恒成立,则
恒成立,则 ,解得
,解得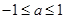

练习册系列答案
相关题目
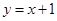 ; (2)
; (2)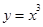 ; (3)
; (3)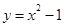 ; (4)
; (4)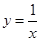 ,
,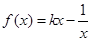 ,且
,且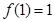 .(1)求实数k的值及函数的定义域;(2)判断函数在(0,+∞)上的单调性
.(1)求实数k的值及函数的定义域;(2)判断函数在(0,+∞)上的单调性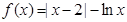 在定义域内的零点的个数为( )
在定义域内的零点的个数为( ) ,则f(x)+f(1-x)=______,并利用推导等差数列前n项和公式的方法,求得f(-5)+f(-4)+···+f(0)+···+f(5)+f(6)的值为________
,则f(x)+f(1-x)=______,并利用推导等差数列前n项和公式的方法,求得f(-5)+f(-4)+···+f(0)+···+f(5)+f(6)的值为________ 的代数式
的代数式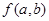 满足:①
满足:①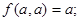 ②
②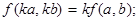
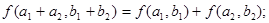 ④
④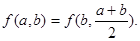
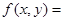 ( )
( )



 及平均价格曲线
及平均价格曲线 (如
(如 是指开始买卖后二个小时的即时价格为3元;
是指开始买卖后二个小时的即时价格为3元; 表示二个小时内的平均价格为3元),在下图给出的四个图像中实线表示
表示二个小时内的平均价格为3元),在下图给出的四个图像中实线表示
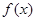 满足
满足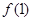 ="1" 且
="1" 且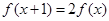 ,则
,则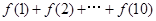 =_________
=_________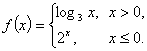 则
则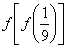 的值为 ( )
的值为 ( )