题目内容
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() 是等边三角形,四边形ABCD是矩形,
是等边三角形,四边形ABCD是矩形,![]() ,F为棱PA上一点,且
,F为棱PA上一点,且![]() ,M为AD的中点,四棱锥
,M为AD的中点,四棱锥![]() 的体积为
的体积为![]() .
.
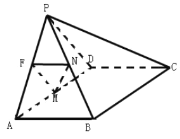
(1)若![]() ,N是PB的中点,求证:平面
,N是PB的中点,求证:平面![]() 平面PCD;
平面PCD;
(2)是否存在![]() ,使得平面FMB与平面PAD所成的二面角余弦的绝对值为
,使得平面FMB与平面PAD所成的二面角余弦的绝对值为![]() .
.
【答案】(1)详见解析(2)存在![]() ,使得平面FMB与平面PAD所成的二面角余弦的绝对值为
,使得平面FMB与平面PAD所成的二面角余弦的绝对值为![]()
【解析】
(1)由已知有![]() ,
,![]() ,即可证明
,即可证明![]() 平面PCD;
平面PCD;
(2)建立以M为原点,MA为x轴,ME为y轴,MP为z轴建立空间直角坐标系![]() ,则可得FMN的法向量为
,则可得FMN的法向量为![]() ,取面PAD的法向量
,取面PAD的法向量![]() ,由向量的数量积公式计算可得解.
,由向量的数量积公式计算可得解.
解:(1)因为![]() ,所以F是AP的中点,又因为N是PB的中点,所以
,所以F是AP的中点,又因为N是PB的中点,所以![]() ,由四边形ABCD是矩形,得
,由四边形ABCD是矩形,得![]() ,故
,故![]() ,
,


 ;
;
(2)连接PM,过M作![]() 交BC于E,由
交BC于E,由![]() 是等边三角形,得
是等边三角形,得![]() ,
, ,以M为原点,MA为x轴,ME为y轴,MP为z轴建立空间直角坐标系
,以M为原点,MA为x轴,ME为y轴,MP为z轴建立空间直角坐标系![]() ,
,

假设存在![]() ,满足题意,设
,满足题意,设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
设面FMN的法向量为![]() ,所以
,所以 ,
,
取![]() ,得
,得![]() ,取面PAD的法向量
,取面PAD的法向量![]() ,
,
由题知: ,解得
,解得![]() ,
,
所以,存在![]() ,使得平面FMB与平面PAD所成的二面角余弦的绝对值为
,使得平面FMB与平面PAD所成的二面角余弦的绝对值为![]()

【题目】某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| n | 0.350 |
第3组 |
| 30 | p |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.000 |
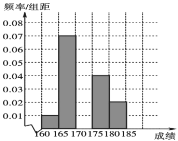
(1)求频率分布表中n,p的值,并估计该组数据的中位数(保留l位小数);
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率.