题目内容
已知集合A={x∈R| ax2-3x+2=0},其中a为常数,且a∈R.
①若A是空集,求a的范围;
②若A中只有一个元素,求a的值;
③若A中至多只有一个元素,求a的范围.
解:①∵A是空集,
∴方程ax2-3x+2=0无实数根.
|
|
②∵A中只有一个元素,
∴方程ax2-3x+2=0只有一个实数根.
当a=0时,方程化为-3x+2=0,只有一个实数根x=![]() ;
;
当a≠0时,令Δ=9-8a=0,得a=![]() ,这时一元二次方程ax2-3x+2=0有两个相等的实数根,即A中只有一个元素.
,这时一元二次方程ax2-3x+2=0有两个相等的实数根,即A中只有一个元素.
由以上可知a=0,或a=![]() 时,A中只有一个元素.
时,A中只有一个元素.
③若A中至多只有一个元素,则包括两种情形:A中有且仅有一个元素;A是空集.由①②的结果可得a=0,或a≥![]() .
.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 ≥1},集合B={x∈R|y=
≥1},集合B={x∈R|y=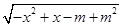 },若A∪B=A,求实数m的取值范围.
},若A∪B=A,求实数m的取值范围.