Question

已知集合A＝{x∈R|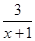≥1}，集合B＝{x∈R|y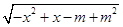＝}，若A∪B＝A，求实数m的取值范围．

 

Answer 1

【答案】

－1＜m＜2.

【解析】

试题分析：解不等式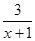≥1求出集合A.要使得函数y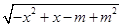＝有意义，则x²－x＋m－m²≤0.

由题设A∪B＝A得关于m的不等式组，解此不等式组便可得m的取值范围.

试题解析：由题意得：A＝{x∈R|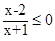}＝(－1,2]，

B＝{x∈R| x²－x＋m－m²≤0}＝{x∈R|(x－m)(x－1＋m)≤ 0}

由A∪B＝A知B⊆A，得－1＜m≤2，－1＜1－m≤2，

解得：－1＜m＜2.

考点：1、集合的运算；2、解不等式；3、函数的定义域.