题目内容
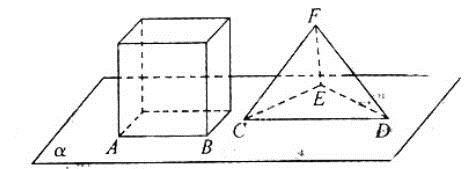
如图,正方体的底面与正四面体的底面在同一平面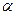 上,且
上,且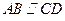 ,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为
,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为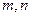 ,那么
,那么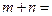 ( )
( )
 上,且
上,且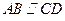 ,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为
,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为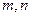 ,那么
,那么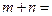 ( )
( )
| A.8 |
| B.9 |
| C.10 |
| D.11 |
A
因为CE在平面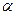 上,所以CE平行于上底面,由于CE与正方体底面各线都相交,所以CE与正方体各侧面相交,即m=4
上,所以CE平行于上底面,由于CE与正方体底面各线都相交,所以CE与正方体各侧面相交,即m=4
设正四面体的高为直线a,则a与正方体各侧棱平行,EF与a所在的平面与正方体的两个侧面平行,所以EF与正方体的两个侧面不相交.由于上下底面,正面与后面都与两侧面相交,所以EF与它们相交,即n=4
∴m+n=8
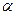 上,所以CE平行于上底面,由于CE与正方体底面各线都相交,所以CE与正方体各侧面相交,即m=4
上,所以CE平行于上底面,由于CE与正方体底面各线都相交,所以CE与正方体各侧面相交,即m=4设正四面体的高为直线a,则a与正方体各侧棱平行,EF与a所在的平面与正方体的两个侧面平行,所以EF与正方体的两个侧面不相交.由于上下底面,正面与后面都与两侧面相交,所以EF与它们相交,即n=4
∴m+n=8

练习册系列答案
相关题目
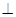 平面ABCD,则点A1的轨迹是( )
平面ABCD,则点A1的轨迹是( )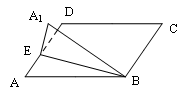
 cm2,已知球心到该截面的距离为1 cm,则该球的体积
cm2,已知球心到该截面的距离为1 cm,则该球的体积
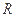 的球面,两个截面圆的半径为
的球面,两个截面圆的半径为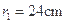 ,
,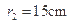 .两截面间的距离为
.两截面间的距离为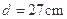 ,求球的表面积( )
,求球的表面积( )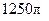
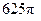
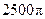
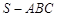 中,
中,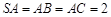 ,
,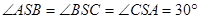 ,
,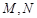 分别为
分别为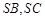 上的点,则
上的点,则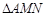 周长最小值为 .
周长最小值为 . 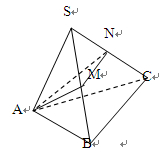
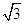 的球面上.若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.
的球面上.若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.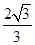 ,则它的外接球的表面积为( )
,则它的外接球的表面积为( )



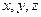 满足
满足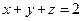 ,求
,求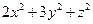 的最小值;
的最小值;