题目内容
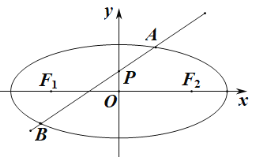
【题目】如图，椭圆
的离心率是
，左右焦点分别为
，
，过点
的动直线
与椭圆相交于
，
两点，当直线过时，
的周长为
.
（1）求椭圆
的方程；
（2）当
时，求直线方程；
（3）已知点
，直线
，
的斜率分别为
，
.问是否存在实数
，使得
恒成立？
【答案】(1) 
(2) 
(3)存在，
【解析】
（1）由焦点三角形的周长特点可求出
值，再结合椭圆离心率是
，可求出
，进而求得椭圆标准方程；
（2），设直线方程为
，
，
，可联立直线方程和椭圆标准方程，得出两根和与积的表达式，再结合
，代换出
与
的关系式；
（3）先用必要性探路，找特殊情况，当
轴可知
，此时存在使得
成立，根据题意和斜率定义表示出
，结合（2）中韦达定理即可得证
（1）由椭圆定义知
的周长为
，
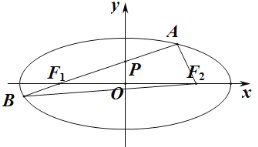
所以
，所以
又离心率
，所以
，所以
所以椭圆
的方程为.
（2）当
轴，
所以可设，，
则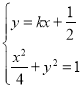
，消去
得
所以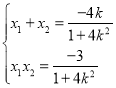
因为，
所以
，即
代入化简得
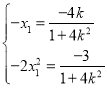所以
解得
所以直线
方程为：，
（3）当轴可知，此时存在使得成立，
下面证明当时恒成立
因为
所以恒成立
即存在，使得恒成立.
【题目】已知某产品的销售额
与广告费用
之间的关系如下表：
| 0 | 1 | 2 | 3 | 4 |
| 10 | 15 |
| 30 | 35 |
若根据表中的数据用最小二乘法求得对的回归直线方程为
，则下列说法中错误的是（ ）
A.产品的销售额与广告费用成正相关
B.该回归直线过点
C.当广告费用为10万元时，销售额一定为74万元
D.
的值是20
【题目】某市《城市总体规划（
年）》提出到
年实现“
分钟社区生活圈”全覆盖的目标，从教育与文化、医疗与养老、交通与购物、休闲与健身
个方面构建“分钟社区生活圈”指标体系，并依据“分钟社区生活圈”指数高低将小区划分为：优质小区（指数为
）、良好小区（指数为
）、中等小区（指数为
）以及待改进小区（指数为
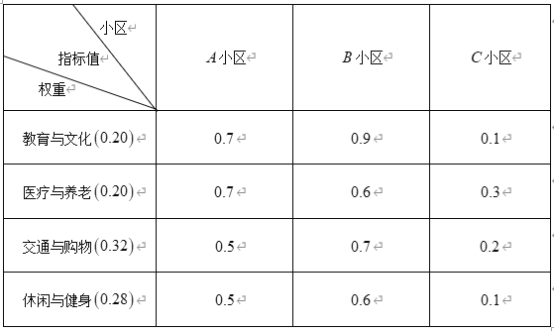
）个等级.下面是三个小区个方面指标的调查数据：
注：每个小区“分钟社区生活圈”指数
，其中
、
、
、
为该小区四个方面的权重，
、
、
、
为该小区四个方面的指标值（小区每一个方面的指标值为
之间的一个数值）.
现有
个小区的“分钟社区生活圈”指数数据，整理得到如下频数分布表：
分组 |
|
|
|
|
|
频数 |
|
|
|
|
|
（Ⅰ）分别判断
、
、
三个小区是否是优质小区，并说明理由；
（Ⅱ）对这个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样，抽取
个小区进行调查，若在抽取的个小区中再随机地选取
个小区做深入调查，记这个小区中为优质小区的个数
，求的分布列及数学期望.
