题目内容
【题目】已知函数f（x）=x|x﹣a|的定义域为D，其中a为常数；
（1）若D=R，且f（x）是奇函数，求a的值；
（2）若a≤﹣1，D=[﹣1，0]，函数f（x）的最小值是g（a），求g（a）的最大值；
（3）若a＞0，在[0，3]上存在n个点xi（i=1，2，…，n，n≥3），满足x1=0，xn=3，x1＜x2＜…＜xn ， 使|f（x1）﹣f（x2）|+|f（x2）﹣f（x3）|+…+|f（xn﹣1）﹣f（xn）|= 
，求实数a的取值．
【答案】
（1）解：∵f（x）是R上的奇函数，
∴f（﹣1）+f（1）=﹣|﹣1﹣a|+|1﹣a|=0，
∴|a﹣1|=|a+1|，解得a=0．
∴f（x）=x|x|，经过验证满足题意
（2）解：a≤﹣1，D=[﹣1，0]，函数f（x）=x（x﹣a）= 
﹣ 
，
①a≤﹣2时，对称轴x= 
≤﹣1，函数f（x）在D上单调递增，
∴f（x）的最小值是f（﹣1）=﹣（﹣1﹣a）=a+1，
则g（a）≤﹣2+1=﹣1，
故g（a）的最大值为﹣1；
②﹣2＜a≤﹣1时，对称轴x= ∈ 
，函数f（x）在（ ，﹣ 
）上单调递增，
在[﹣1， ]单调递减；
∴f（x）的最小值是f（ ）=﹣ ，
则g（a）≤﹣ 
，
故g（a）的最大值为﹣
（3）解：a＞0，函数f（x）=x|x﹣a|的图象可由f（x）=x|x|的图象右移a个单位得到．
而f（x）=x|x|=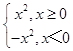 
，x＞0时递增，x＜0时递增，且f（x）的图象连续，
则函数f（x）=x|x﹣a|在[0，3]递增，
即有|f（x1）﹣f（x2）|+|f（x2）﹣f（x3）|+…+|f（xn﹣1）﹣f（xn）|= 
，
化为﹣（f（x1）﹣f（x2）+f（x2）﹣f（x3）+…+f（xn﹣1）﹣f（xn））= ，
即﹣（f（0）﹣f（3））= ，
则3|3﹣a|﹣0= ，
解得a= 
或 
．
则实数a的取值为{ ， }
【解析】（1）由奇函数的定义可得f（﹣1）+f（1）=0，解得a=0，即可得到f（x）的解析式；（2）化简f（x），对a讨论，①a≤﹣2时，②﹣2＜a≤﹣1时，由二次函数对称轴，结合单调性即可得到最值；（3）a＞0，函数f（x）=x|x﹣a|的图象可由f（x）=x|x|的图象右移a个单位得到．判断f（x）=x|x|在R上递增，可得函数f（x）=x|x﹣a|在[0，3]递增，去掉绝对值，化简整理计算即可得到a的取值．
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识，掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值，以及对函数的奇偶性的理解，了解偶函数的图象关于y轴对称；奇函数的图象关于原点对称．
