题目内容
【题目】一个大于1的自然数,除了1和它本身外,不能被其他自然数整除,则称这个数为质数.质数的个数是无穷的.设由所有质数组成的无穷递增数列![]() 的前
的前![]() 项和为
项和为![]() ,等差数列1,3,5,7,…中所有不大于
,等差数列1,3,5,7,…中所有不大于![]() 的项的和为
的项的和为![]() .
.
(Ⅰ)求![]() 和
和![]() ;
;
(Ⅱ)判断![]() 和
和![]() 的大小,不用证明;
的大小,不用证明;
(Ⅲ)设![]() ,求证:
,求证:![]() ,
,![]() ,使得
,使得![]() .
.
【答案】(Ⅰ)11,36 (Ⅱ)见解析;(Ⅲ)见解析.
【解析】
(Ⅰ)由题意直接求得p5和f(5);
(Ⅱ)分别取n=1,2,3,4,5.求得Sn和f(n),比较大小得结论;
(Ⅲ)取值验证n≤4时,命题成立.当n≥5时,设k是使得k2≤Sn成立的最大自然数,只需证(k+1)2<Sn+1.可得![]() 1+3+5+…+(2k﹣1),f(n)=1+3+5+…+pn,结合(Ⅱ)可知,当n≥5时,Sn<f(n),得到pn>2k﹣1,从而pn+1>2k+1.进一步得到
1+3+5+…+(2k﹣1),f(n)=1+3+5+…+pn,结合(Ⅱ)可知,当n≥5时,Sn<f(n),得到pn>2k﹣1,从而pn+1>2k+1.进一步得到![]() .
.
(Ⅰ)![]() ,
,
![]() ;
;
(Ⅱ)当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,
,![]() .
.
所以当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,![]() .
.
不难看出,当![]() 时,
时,![]() .
.
(Ⅲ)因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ,使得
,使得![]() ;
;
当![]() 时,
时,![]() ,使得
,使得![]() ;
;
当![]() 时,
时,![]() ,使得
,使得![]() ;
;
当![]() 时,
时,![]() ,使得
,使得![]()
所以![]() 时,命题成立.
时,命题成立.
当![]() 时,设
时,设![]() 是使得
是使得![]() 成立的最大自然数,只需证
成立的最大自然数,只需证![]() .
.
因为![]()
![]() ,
,
![]() ,
,
由(Ⅱ)可知,当![]() 时,
时,![]() ,
,
所以![]() ,从而
,从而![]()
所以![]() ,即
,即![]() .
.
综上可知,命题成立.

【题目】某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图,将使用手机时间不低于80分钟的学生称为“手机迷”.
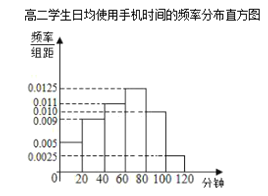
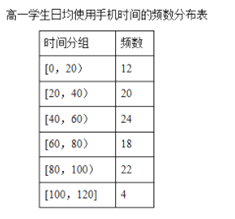
(I)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(II)在高二的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
非手机迷 | 手机迷 | 合计 | |
男 | |||
女 | |||
合计 |
附:随机变量![]() (其中
(其中![]() 为样本总量).
为样本总量).
参考数据 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
【题目】某公司培训员工某项技能,培训有如下两种方式,方式一:周一到周五每天培训1小时,周日测试;方式二:周六一天培训4小时,周日测试.公司有多个班组,每个班组60人,现任选两组(记为甲组、乙组)先培训,甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如下表,其中第一、二周达标的员工评为优秀.
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
(1)在甲组内任选两人,求恰有一人优秀的概率;
(2)每个员工技能测试是否达标相互独立,以频率作为概率.
(i)设公司员工在方式一、二下的受训时间分别为![]() 、
、![]() ,求
,求![]() 、
、![]() 的分布列,若选平均受训时间少的,则公司应选哪种培训方式?
的分布列,若选平均受训时间少的,则公司应选哪种培训方式?
(ii)按(i)中所选方式从公司任选两人,求恰有一人优秀的概率.
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为![]() 的样本,得到一周参加社区服务的时间的统计数据好下表:
的样本,得到一周参加社区服务的时间的统计数据好下表:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(Ⅲ)以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,现从该校学生中随机调查6名学生,试估计6名学生中一周参加社区服务时间超过1小时的人数.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()