题目内容
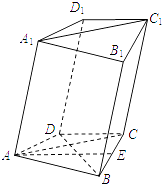
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE,设PA=1,AD=2.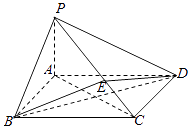
(1)求平面BPC的法向量;
(2)求二面角B﹣PC﹣A的正切值.
【答案】
(1)解:∵PA⊥平面ABCD,BD平面ABCD,
∴PA⊥BD.
∵PC⊥平面BDE,BD平面BDE,∴PC⊥BD.
又PA∩PC=P,∴BD⊥平面PAC,AC平面PAC,
∴BD⊥AC.
又底面ABCD为矩形,∴ABCD为正方形.
建立如图所示的空间直角坐标系.
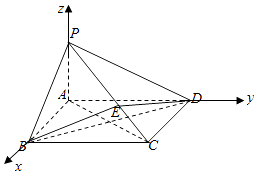
A(0,0,0),B(2,0,0),C(2,2,0),P(0,0,1),
D(0,2,0).
![]() =(0,2,0),
=(0,2,0), ![]() =(﹣2,0,1),
=(﹣2,0,1),
设平面BPC的法向量为 ![]() =(x,y,z),
=(x,y,z),
∴ 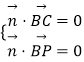 ,∴
,∴ ![]() ,取
,取 ![]() =(1,0,2).
=(1,0,2).
∴平面BPC的一个法向量为 ![]() =(1,0,2).
=(1,0,2).
(2)平面PAC的法向量为: ![]() =(﹣2,2,0).
=(﹣2,2,0).
设二面角B﹣PC﹣A=θ,由图可知:θ为锐角.
则cos ![]() =
= ![]() =
= ![]() =﹣
=﹣ ![]() .
.
∴cosθ= ![]() .
.
∴sinθ= ![]() .
.
∴tanθ= ![]() =3.即二面角B﹣PC﹣A的正切值为3.
=3.即二面角B﹣PC﹣A的正切值为3.
【解析】(1)先利用线面垂直的判定定理可证BD⊥平面PAC,进而可证BD⊥AC,从而可证ABCD为正方形,再建立空间直角坐标系,设平面BPC的法向量,利用平面向量的数量积等于0可得平面BPC的一个法向量;(2)先计算平面PAC的法向量,再设二面角B﹣PC﹣A=θ,可得cosθ,进而利用同角三角函数的基本关系可得tanθ,即二面角B﹣PC﹣A的正切值.
【考点精析】解答此题的关键在于理解平面的法向量的相关知识,掌握若向量![]() 所在直线垂直于平面
所在直线垂直于平面![]() ,则称这个向量垂直于平面
,则称这个向量垂直于平面![]() ,记作
,记作![]() ,如果
,如果![]() ,那么向量
,那么向量![]() 叫做平面
叫做平面![]() 的法向量.
的法向量.

练习册系列答案
相关题目