题目内容
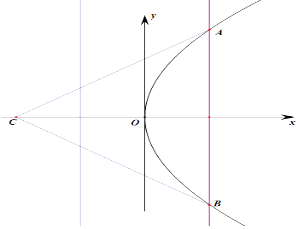
【题目】已知抛物线y2=2px(p>0),过点C(﹣4,0)作抛物线的两条切线CA,CB,A,B为切点,若直线AB经过抛物线y2=2px的焦点,△CAB的面积为24,则以直线AB为准线的抛物线标准方程是( )
A.y2=4x
B.y2=﹣4x
C.y2=8x
D.y2=﹣8x
【答案】D
【解析】解:由抛物线的对称性知,AB⊥x轴,且AB是焦点弦,故丨AB丨=2p,
∴△CAB的面积S= ![]() ×丨AB丨×d=
×丨AB丨×d= ![]() ×2p×(
×2p×( ![]() +4)=24,整理得:p2+8p﹣48=0,
+4)=24,整理得:p2+8p﹣48=0,
解得p=4,或p=﹣12(舍去),
∴p=4,则抛物线方程y2=8x,
∴AB的方程:x=2,
∴以直线AB为准线的抛物线标准方程y2=﹣8x,
故选D.
由抛物线性质得出AB=2p,由面积可得出p的值,最终得出抛物线的标准方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在“新零售”模式的背景下,某大型零售公司推广线下分店,计划在S市的A区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这x个分店的年收入之和.
x(个) | 2 | 3 | 4 | 5 | 6 |
y(百万元) | 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程 ![]() ;
;
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为z=y﹣0.05x2﹣1.4,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
(参考公式: ![]() ,其中
,其中 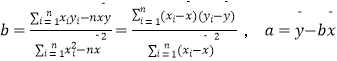 )
)