题目内容
【题目】平面直角坐标系xOy中,椭圆C: ![]() 的离心率是
的离心率是 ![]() ,
,
抛物线E:x2=4y的焦点F是C的一个顶点.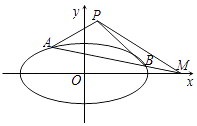
(1)求椭圆C的方程;
(2)设与坐标轴不重合的动直线l与C交于不同的两点A和B,与x轴交于点M,且 ![]() 满足kPA+kPB=2kPM , 试判断点M是否为定点?若是定点求出点M的坐标;若不是定点请说明理由.
满足kPA+kPB=2kPM , 试判断点M是否为定点?若是定点求出点M的坐标;若不是定点请说明理由.
【答案】
(1)解:由抛物线E:x2=4y,得F(0,1),即b=1,
又 ![]() ,a2=b2+c2=1+c2,
,a2=b2+c2=1+c2,
解得:a=2,c= ![]() .
.
∴椭圆方程为 ![]() ;
;
(2)设直线l:x=my+t,A(x1,y1),B(x2,y2),则M(t,0),
由 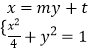 得(m2+4)y2+2mty+t2﹣4=0,
得(m2+4)y2+2mty+t2﹣4=0,
△=16m2﹣16t2+64>0
![]() ,
,
![]() =
= ![]() ,x1x2=(my1+t)(my2+t)=
,x1x2=(my1+t)(my2+t)= ![]()
y1x2+y2x1=2my1y2+t(y1+y2)= ![]()
由kPA+kPB=2kPM,得 ![]()
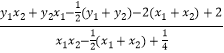 =
= ![]() .
.
2t2+(4m﹣17)t﹣32m+8=02t2﹣17t+8+m(4t﹣32)=0
当t=8时,2t2﹣17t+8+m(4t﹣32)=0恒成立,
故M为定点(8,0).
【解析】(1)利用已知条件可得含有a,c的方程组,解方程组可得a,c,进而可得b,从而可得椭圆C的方程;(2)设直线l,A,B的坐标,联立直线l方程和椭圆C的方程,消去x,可得y1+y2,y1y2,进而可得x1+x2,x1x2,由kPA+kPB=2kPM可得关于m的方程,进而可得t,从而可得点M的坐标.

练习册系列答案
相关题目