题目内容
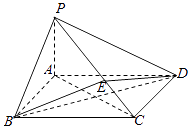
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且 ![]() ,AD=CD=1.
,AD=CD=1.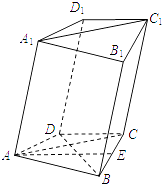
(1)求证:BD⊥AA1;
(2)若E为棱BC的中点,求证:AE∥平面DCC1D1 .
【答案】
(1)证明:∵AB=BC,AD=CD,∴BD垂直平分AC,
∵平面AA1C1C⊥平面ABCD,
∴BD⊥平面AA1C1C,
∴BD⊥AA1;
(2)是BD∩AC=O,则OC= ![]() ,
,
又DC=1,∴ ![]() =
= ![]() ,∴∠OCD=30°.
,∴∠OCD=30°.
∵∠ACB=60°,∴∠BCD=90°.
∴DC⊥BC.
∵E为等边三角形的边BC的中点,∴AE⊥BC,∴DC∥AE.
∵AE平面DCC1D1.DC平面DCC1D1.
∴AE∥平面DCC1D1.
【解析】(1)由中垂线定理可得![]() ,结合面面垂直不难得出
,结合面面垂直不难得出![]() ,进而得证;(2)根据题上所给长度,由边角关系不难得出
,进而得证;(2)根据题上所给长度,由边角关系不难得出![]() ,又由等边三角形三线合一可得
,又由等边三角形三线合一可得![]() ,所以
,所以![]() ,
,![]() 在面内,结论得证
在面内,结论得证

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】随着雾霾日益严重,很多地区都实行了“限行”政策,现从某地区居民中,随机抽取了300名居民了解他们对这一政策的态度,绘成如图所示的2×2列联表:
反对 | 支持 | 合计 | |
男性 | 70 | 60 | |
女性 | 50 | 120 | |
合计 |
(1)试问有没有99%的把握认为对“限行”政策的态度与性别有关?
(2)用样本估计总体,把频率作为概率,若从该地区所有的居民(人数很多)中随机抽取3人,用ξ表示所选3人中反对的人数,试写出ξ的分布列,并求出ξ的数学期望.
K2= ![]() ,其中n=a+b+c+d独立性检验临界表:
,其中n=a+b+c+d独立性检验临界表:
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |