题目内容
16.已知正弦函数f(x)=sinx.下列说法不正确的是( )| A. | 函数y=f(x)的图象与函数y=$\frac{1}{π-x}$的图象在[0,2π]上所有交点的横坐标之和为4π | |
| B. | ?x∈[0,+∞),f(x)≤x | |
| C. | 若函数y=f(x)的图象的两条相互垂直的切线交于P点,则点P的坐标可能为($\frac{π}{2}$,$\frac{π}{2}$) | |
| D. | 若函数y=f(x)的图象的两条相互垂直的切线交于P点,则点P的坐标可能为($\frac{3π}{2}$,$\frac{π}{2}$) |
分析 A.作出两个函数的图象,得到两个函数都关于点(π,0)对称,利用对称性进行求解判断.
B.构造函数g(x)=f(x)-x=sinx-x,求函数的导数,利用导数判断函数的单调性即可得到结论.
C.D若l1,l2是函数f(x)=sinx图象上的任意两条相互垂直的切线,设这两个切点的横坐标分别为x1、x2,则cosx1cosx2=-1,即切点的横坐标等于kπ,纵坐标为0.求出相邻的两条切线方程,解方程组求出两切线交点的坐标,检验可得结论.
解答 解:A.作出函数y=$\frac{1}{π-x}$的图象,则函数关于点(π,0)对称,
同时点(π,0)也是函数y=sinx(0≤x≤2π)的对称点,
由图象可知,两个函数在[0,2π]上共有4个交点,两两关于点(π,0)对称,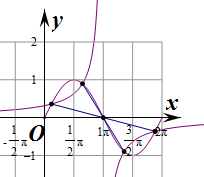
设对称的两个点的横坐标分别为x1,x2,
则x1+x2=2×π=2π,
∴4个交点的横坐标之和为2×2π=4π.故A正确,
B.设g(x)=f(x)-x=sinx-x,
则g′(x)=cosx-1≤0,即当x≥0时,函数g(x)单调递增,
则g(x)≤g(0)=0,即?x∈[0,+∞),f(x)≤x成立,故B正确,
C.由f(x)=sinx,得f′(x)=cosx,若l1,l2是函数f(x)=sinx图象上的任意两条相互垂直的切线,
设这两个切点的横坐标分别为x1、x2,则cosx1cosx2=-1.
不妨设cosx1≤cosx2,则必有cosx1=-1,cosx2=1,故切点的横坐标等于kπ,纵坐标为0.
由于所给选项纵坐标比较小,故这两条切线必为相邻两条互相垂的切线.
不妨设切线的斜率等于1的切线对应的一个切点为A(0,0),则另一个切线的斜率为-1.
①当另一个切点为B(-π,0),则两条切线的方程分别为y=x、y=-1(x+π),
可得此时这两条切线的交点为(-$\frac{π}{2}$,-$\frac{π}{2}$).
②当另一个切点为C(π,0),则两条切线的方程分别为y=x、y=-1(x-π),
可得此时这两条切线的交点为($\frac{π}{2}$,$\frac{π}{2}$).
③若斜率等于1的切线对应的一个切点为E(2π,0),当另一个切点为C(π,0),
则两条切线的方程分别为y=x-2π、y=-1(x-π),
可得此时这两条切线的交点为($\frac{3π}{2}$,-$\frac{π}{2}$).
故C正确,D错误,
故选:D
点评 本题主要考查与正弦函数有关的命题的真假判断,涉及的内容较多,综合性较强,难度较大.

| n | 1 | 2 | 3 | 4 | 5 | 6 |
| xn | 70 | 76 | 72 | 70 | 72 | x6 |
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{2}{3}$ | D. | -1 |
p1:?x0∈(-∞,0),4${\;}^{{x}_{0}}$<5${\;}^{{x}_{0}}$,
p2:在锐角三角形ABC中,若tanA>tanB,则A>B;
p3:?x∈R,cosx0≥1;
p4:?x∈R,x2-x+1>0
其中假命题是( )
| A. | p1 | B. | p2 | C. | p3 | D. | p4 |
| A. | (-6,0] | B. | [-6,0) | C. | (-1,0) | D. | [-1,0] |