题目内容
4.O为?ABCD所在平面上一点,若$\frac{|\overrightarrow{AB|}}{|\overrightarrow{AD|}}$=$\frac{2}{3}$,$\overrightarrow{OA}$+$\overrightarrow{OB}$=λ($\overrightarrow{OC}$+$\overrightarrow{OD}$),$\overrightarrow{OA}$=μ($\overrightarrow{AB}$+2$\overrightarrow{AC}$),则λ的值是( )| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{2}{3}$ | D. | -1 |
分析 利用平行四边形的性质、三角形中位线定理、平行线分线段成比例定理即可得出.
解答 解:如图所示,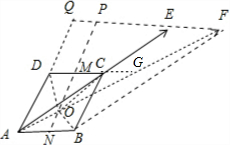 延长AC到点E,使得AE=2AC,以AE,AB为邻边作一个平行四边形ABFE,连接对角线AF.
延长AC到点E,使得AE=2AC,以AE,AB为邻边作一个平行四边形ABFE,连接对角线AF.
分别取AB,CD的中点N,M.
由$\overrightarrow{OA}$+$\overrightarrow{OB}$=λ($\overrightarrow{OC}$+$\overrightarrow{OD}$),$\overrightarrow{OA}$=μ($\overrightarrow{AB}$+2$\overrightarrow{AC}$),
可知:点O是AF与NM的交点.
直线EF与NM相交于点P,直线EF与AD相交与点Q,直线DC与AF相交于点G.
∵$\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{ON}$,$\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{OM}$,
∴$\overrightarrow{ON}=λ\overrightarrow{OM}$.
∵若$\frac{|\overrightarrow{AB|}}{|\overrightarrow{AD|}}$=$\frac{2}{3}$,
∴不妨设|$\overrightarrow{AB}$|=2,则|$\overrightarrow{AD}$|=3,
∵点C是线段AE的中点,
∴EQ=4,PQ=1,EP=3.
∴$\frac{ON}{OP}=\frac{AN}{FP}$=$\frac{1}{5}$,
∵G为AF的中点,
∴CG=$\frac{1}{2}$EF=1.
∴$\frac{OM}{OP}=\frac{MG}{FP}$=$\frac{2}{5}$,
∴$\frac{ON}{OM}=\frac{1}{2}$,
∴$λ=-\frac{1}{2}$.
故选:B.
点评 本题考查了向量的平行四边形法则、向量共线定理、平行四边形的性质、三角形中位线定理、平行线分线段成比例定理,考查了推理能力与计算能力,难度较大.

| A. | $\sqrt{13}$ | B. | $\frac{{\sqrt{13}}}{5}$ | C. | $\sqrt{65}$ | D. | $\frac{{\sqrt{65}}}{5}$ |
| A. | 函数y=f(x)的图象与函数y=$\frac{1}{π-x}$的图象在[0,2π]上所有交点的横坐标之和为4π | |
| B. | ?x∈[0,+∞),f(x)≤x | |
| C. | 若函数y=f(x)的图象的两条相互垂直的切线交于P点,则点P的坐标可能为($\frac{π}{2}$,$\frac{π}{2}$) | |
| D. | 若函数y=f(x)的图象的两条相互垂直的切线交于P点,则点P的坐标可能为($\frac{3π}{2}$,$\frac{π}{2}$) |