题目内容
已知 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
.
(Ⅰ)求函数 的表达式;
的表达式;
(Ⅱ)求数列 的前
的前 项和
项和 .
.
(1)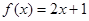 ;(2)
;(2) .
.
解析试题分析:本题是三角函数和数列的一道综合题,考查二倍角公式、特殊角函数值以及等比数列的通项公式和错位相减法求和等基础知识,考查分析问题、解决问题的能力,考查计算能力.第一问,因为表达式中有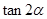 ,而已知
,而已知 ,正好符合二倍角公式,所以先利用这个公式求出
,正好符合二倍角公式,所以先利用这个公式求出 ,由于
,由于 为锐角,而
为锐角,而 ,所以
,所以 ,将角代入
,将角代入 中,可以求出
中,可以求出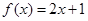 ;第二问,先利用构造法构造一个等比数列
;第二问,先利用构造法构造一个等比数列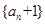 ,利用等比数列的通项公式,求出
,利用等比数列的通项公式,求出 ,再求
,再求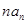 ,要求
,要求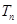 ,先把
,先把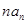 分开用2部分表示,一部分符合错位相减法,另一部分是等差数列,最后把这2部分的和加在一起即可.
分开用2部分表示,一部分符合错位相减法,另一部分是等差数列,最后把这2部分的和加在一起即可.
试题解析:⑴ 又∵
又∵ 为锐角,
为锐角,
∴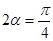 ∴
∴
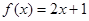 5分
5分
(2) ∵ , ∴
, ∴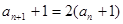
∵ ∴数列
∴数列 是以2为首项,2为公比的等比数列。
是以2为首项,2为公比的等比数列。
可得 ,∴
,∴ , 9分
, 9分
所以,
下面先求 的前
的前 项和
项和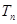

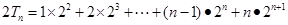
两式相减,得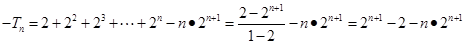

 12分
12分
12分
考点:1.二倍角公式;2.特殊角的三角函数值;3.构造法求通项公式;4.错位相减法;5.分组求和;6.等差、等比数列的求和公式.

练习册系列答案
相关题目
 的图象(部分)如图所示.
的图象(部分)如图所示.
 的解析式;
的解析式; ,求函数
,求函数 <C<
<C< ,且
,且 =
= .
. +
+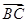 |=2,求
|=2,求 在一个周期内的图象如图所示,点
在一个周期内的图象如图所示,点 为图象的最高点,
为图象的最高点, 为图象与
为图象与 轴的交点,且三角形
轴的交点,且三角形 的面积为
的面积为 .
.
 的值及函数
的值及函数 的值域;
的值域; ,求
,求 的值.
的值.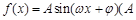 >0,
>0, >0,
>0,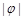 <
< 的图像与
的图像与 轴的交点为(0,1),它在
轴的交点为(0,1),它在 和
和
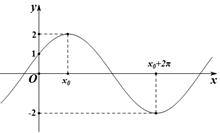
 的解析式及
的解析式及 的值;
的值; 满足
满足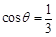 ,求
,求 的值.
的值.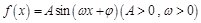 的一段图象如图所示.
的一段图象如图所示.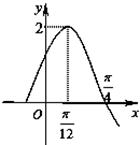
 的解析式;
的解析式; 求函数
求函数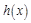 的单调递增区间.
的单调递增区间. ,
,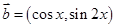 ,
,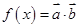 .(1)求
.(1)求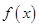 的最小正周期、最大值及
的最小正周期、最大值及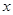 的集合;
的集合;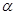 满足
满足 ,求
,求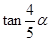 的值.
的值. (其中
(其中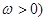 的最小正周期为
的最小正周期为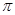 .
.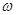 的值,并求函数
的值,并求函数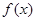 的单调递减区间;
的单调递减区间;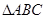 中,
中, 分别是角
分别是角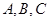 的对边,若
的对边,若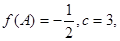
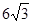 ,求
,求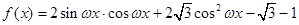 (其中
(其中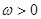 ),
),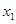 、
、 是函数
是函数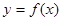 的两个不同的零点,且
的两个不同的零点,且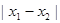 的最小值为
的最小值为 .
. 的值;
的值;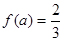 ,求
,求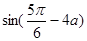 的值.
的值.