题目内容
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,顶点为
,顶点为![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是椭圆
是椭圆![]() 上除顶点外的任意一点,直线
上除顶点外的任意一点,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .设
.设![]() 的斜率为
的斜率为![]() ,
,![]() 的斜率为
的斜率为![]() ,试问
,试问![]() 是否为定值?并说明理由.
是否为定值?并说明理由.
【答案】(1) 椭圆![]() 的方程为:
的方程为:![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(Ⅰ)由椭圆的离心率![]() ,
,![]() ,列出方程组,求出a,b,由此能求出椭圆C的方程.
,列出方程组,求出a,b,由此能求出椭圆C的方程.
(Ⅱ)由A1(-2,0)、A2(2,0)、B1(0,-1)、B2(0,1),得直线A2P的方程为![]() ,由
,由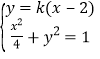 ,得
,得![]() ,由此利用韦达定理、直线方程、直线的斜率公式,结合已知条件能求出2m-k为定值.
,由此利用韦达定理、直线方程、直线的斜率公式,结合已知条件能求出2m-k为定值.
试题解析:
(Ⅰ)解:∵![]() ,∴
,∴![]() ,即
,即![]() ①
①
由已知,A1(-a,0)、A2(a,0)、B1(0,-b)、B2(0,b)
∴![]()
由![]() 得
得![]() ②
②
由①②得:a = 2,b = 1,∴椭圆C的方程为![]() .
.
(Ⅱ)证:由(Ⅰ)知,A1(-2,0)、A2(2,0)、B1(0,-1)、B2(0,1)
∴直线A2P的方程为![]()
由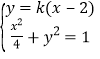 得:
得:![]()
设P(x1,y1),则![]() ,∴
,∴![]()
直线B2P的方程为![]() ,即
,即![]()
令y = 0,得![]() ,即
,即![]()
直线A1B2的方程为![]()
由![]() 得:
得:![]()
∴直线EQ的斜率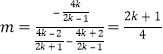 ,∴
,∴![]() ,是定值.
,是定值.

练习册系列答案
相关题目
【题目】从某工厂的一个车间抽取某种产品![]() 件,产品尺寸(单位:
件,产品尺寸(单位:![]() )落在各个小组的频数分布如下表:
)落在各个小组的频数分布如下表:
数据分组 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)根据频数分布表,求该产品尺寸落在![]() 的概率;
的概率;
(2)求这![]() 件产品尺寸的样本平均数
件产品尺寸的样本平均数![]() ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
(3)根据频数分布对应的直方图,可以认为这种产品尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经过计算得
,经过计算得![]() ,利用该正态分布,求
,利用该正态分布,求![]() .
.
附:①若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ;②
;②![]() .
.