Question

【题目】已知二次函数g（x）＝ax2+c（a，c∈R），g（1）＝1且不等式g（x）≤x2﹣x+1对一切实数x恒成立．

（Ⅰ）求函数g（x）的解析式；

（Ⅱ）在（Ⅰ）的条件下，设函数h（x）＝2g（x）﹣2，关于x的不等式h（x﹣1）+4h（m）≤h（）﹣4m2h（x），在x∈[，+∞）有解，求实数m的取值范围．

Answer 1

【答案】（Ⅰ）g（x）；（Ⅱ）[，0）∪（0，]

【解析】

（Ⅰ）先将g（1）＝1代入得a+c＝1，再由g（x）≤x2﹣x+1对一切实数x恒成立转化为

（a﹣1）x2+x+c﹣1≤0对一切实数x恒成立，分类讨论即可求解；

（Ⅱ）先将不等式作变形处理，可得4m2≥1. 在x∈[，+∞）有解，即等价于4m2≥（1 ）min，设y＝1，求得的最小值，再解关于的不等式即可；

（Ⅰ）∵二次函数g（x）＝ax2+c（a，c∈R），g（1）＝1；∴a+c＝1①；

又∵不等式g（x）≤x2﹣x+1对一切实数x恒成立；∴（a﹣1）x2+x+c﹣1≤0对一切实数x恒成立；

当a﹣1＝0时，x+c﹣1≤0不恒成立，∴a＝1不合题意，舍去；

当a﹣1≠0时，要使得（a﹣1）x2+x+c﹣1≤0对一切实数x恒成立，

需要满足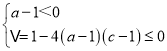：；②，∴由①②解得a，c；

故函数g（x）的解析式为：g（x）．

（Ⅱ）把g（x）代入函数h（x）＝2g（x）﹣2；得h（x）＝x2﹣1；

则关于x的不等式h（x﹣1）+4h（m）≤h（）﹣4m2h（x）在x∈[，+∞）有解，

得，4m2≥1. 在x∈[，+∞）有解；

只要使得4m2≥（1）min；设y＝1，x∈[，+∞），

则y＝﹣3（）2，（0，]，∴当时，ymin；所以，4m2，

解得0＜m2；∴m＜0或0＜m；

故实数m的取值范围为[，0）∪（0，]．