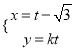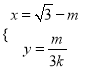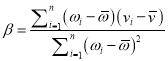题目内容
【题目】已知椭圆![]() 的左右焦点分别是
的左右焦点分别是![]() ,椭圆C的上顶点到直线
,椭圆C的上顶点到直线![]() 的距离为
的距离为![]() ,过
,过![]() 且垂直于x轴的直线与椭圆C相交于M,N两点,
且垂直于x轴的直线与椭圆C相交于M,N两点,
且|MN|=1。
(I)求椭圆![]() 的方程;
的方程;
(II)过点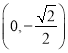 的直线与椭圆C相交于P,Q两点,点
的直线与椭圆C相交于P,Q两点,点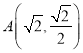 ),且
),且![]() ,求直线
,求直线![]() 的方程。
的方程。
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】试题分析:
(Ⅰ)由![]() 得
得![]() ,由
,由![]() 得
得![]() ,故
,故![]() ,求解方程组有
,求解方程组有![]() ,
, ![]() ,则椭圆
,则椭圆![]() 的方程为
的方程为![]() ;
;
(Ⅱ)设直线![]() 方程为
方程为![]() ,与椭圆
,与椭圆![]() 的方程联立可得
的方程联立可得![]() ,则
,则![]() ,利用平面向量垂直的充要条件有
,利用平面向量垂直的充要条件有![]() ,据此可得关于实数k的方程
,据此可得关于实数k的方程![]() ,解得
,解得![]() 或
或![]() ,经检验当
,经检验当![]() 不合题意,则直线
不合题意,则直线![]() 的方程为
的方程为![]() .
.
试题解析:
(Ⅰ)由点到直线距离公式有![]() ,整理可得
,整理可得![]() ,
,
由通径公式有![]() ,整理可得
,整理可得![]() ,
,
故![]() ,
, ![]() ,
,
![]() ,
, ![]() 椭圆
椭圆![]() 的方程为
的方程为![]() ;
;
(Ⅱ)设直线![]() 方程为
方程为![]() ,与椭圆
,与椭圆![]() 的方程联立消去
的方程联立消去![]() 得
得
![]() ,设
,设![]() ,则
,则![]() ,
,
由![]() 得
得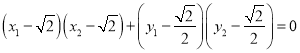 ,即
,即
![]() ,即
,即![]() ,
,
![]() ,即
,即![]() ,解得
,解得![]() 或
或![]()
当![]() 时,直线
时,直线![]() 经过
经过![]() 点,不满足题意,舍去,故
点,不满足题意,舍去,故![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目