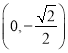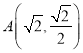题目内容
【题目】知函数![]() (
(![]() 、
、![]() 为常数),曲线
为常数),曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() .
.
(1)求![]() 、
、![]() 的值
的值
(2)求![]() 的最大值
的最大值
(3)设![]() ,证明:对任意
,证明:对任意![]() ,都有
,都有![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)证明过程详见解析
(3)证明过程详见解析
【解析】
(1)由![]() ,及
,及![]() ,解出
,解出![]() 、
、![]() 的值;
的值;
(2)求![]() ,得
,得![]() 的单调性,求出最值;
的单调性,求出最值;
(3)对任意![]() ,
, ![]() 等价于
等价于![]() ,
,
令 ![]() ,可求得
,可求得![]() 的最大值为
的最大值为![]() ,
,
即 ![]() .
.
设![]() ,可得
,可得![]() ,即
,即![]() ,
,
![]() ,命题得证
,命题得证
解:(1)由![]() ,得
,得![]() ,
,
由已知得![]() ,解得
,解得![]() .
.
又![]() .
.
(2)由(1)得: ![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() ;
;
当![]() 时,
时, ![]() ,所以
,所以![]() ,
,
∴当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ,
,
![]() 时,
时, ![]() .
.
(3)证明:![]() .
.
对任意![]() ,
, ![]() 等价于
等价于![]() ,
,
令 ![]() ,则
,则 ![]() ,
,
由 ![]() 得:
得: ![]() ,
,
∴当 ![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() 单调递减,
单调递减,
所以![]() 的最大值为
的最大值为![]() ,即
,即 ![]() .
.
设![]() ,则
,则 ![]() ,
,
∴当![]() 时,
时, ![]() 单调递增,
单调递增, ![]() ,故当
,故当 ![]() 时,
时, ![]() ,即
,即![]() ,
, ![]() ,
,
∴对任意![]() ,都有
,都有 ![]() .
.

【题目】某研究机构对某校高二文科学生的记忆力x和判断力y进行统计分析,得下表数据.
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
参考公式: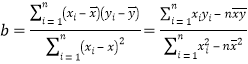
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
【题目】为研究某种图书每册的成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
(千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
15.25 | 3.63 | 0.269 | 2085.5 |
| 0.787 | 7.049 |
表中![]() ,
, ![]() .
.
(1)根据散点图判断: ![]() 与
与![]() 哪一个更适宜作为每册成本费
哪一个更适宜作为每册成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的回归方程类型?(只要求给出判断,不必说明理由)
(千册)的回归方程类型?(只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)若每册书定价为10元,则至少应该印刷多少册才能使销售利润不低于78840元?(假设能够全部售出,结果精确到1)
(附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, ![]() )
)