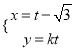题目内容
【题目】已知
，在区间
上存在三个不同的实数
，使得以
为边长的三角形是直角三角形，则
的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】f（x）=x3﹣3x+2+m，求导f′（x）=3x2﹣3由f′（x）=0得到x=1或者x=﹣1，
又x在[0，2]内，∴函数f（x）在区间（0，1）单调递减，在区间（1，2）单调递增，
则f（x）min=f（1）=m，f（x）max=f（2）=m+4，f（0）=m+2．
∵在区间[0，2]上存在三个不同的实数a，b，c，使得以f（a），f（b），f（c）为边长的三角形是构成直角三角形，
∴2m2＜（m+4）2，即m2﹣8m﹣16＜0，解得4﹣
＜m＜4+
，
又已知m＞0，∴0＜m＜4+
．
故选：D．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌，得到如下
列联表：
男生 | 女生 | 合计 | |
挑同桌 | 30 | 40 | 70 |
不挑同桌 | 20 | 10 | 30 |
总计 | 50 | 50 | 100 |
Ⅰ
从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本，现从这5人中随机选取3人做深度采访，求这3名学生中至少有2名要挑同桌的概率；
Ⅱ
根据以上
列联表，是否有
以上的把握认为“性别与在选择座位时是否挑同桌”有关？
下面的临界值表供参考：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式： 
，其中
