题目内容
(12分)在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
附: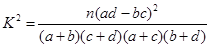 ;
;
 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)列联表见解析(2)有97.5%的把握认为“休闲方式与性别有关”
解析试题分析:(1)2×2的列联表
……5分休闲方式
性别看电视 运动 总计 女 43 27 70 男 21 33 54 总计 64 60 124
(2)假设“休闲方式与性别无关”
计算 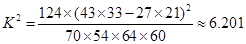 ……10分
……10分
因为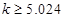 ,所以有理由认为假设“休闲方式与性别无关”是不合理的,
,所以有理由认为假设“休闲方式与性别无关”是不合理的,
有97.5%的把握认为“休闲方式与性别有关”. ……12分
考点:本小题主要考查2×2列联表的绘制和应用以及独立性检验的应用.
点评:2×2列联表在独立性检验中很有用,要灵活应用;另外第(2)问是有比较大的把握认为“休闲方式与性别无关”,而不是直接答有关还是无关.

(本小题满分12分)
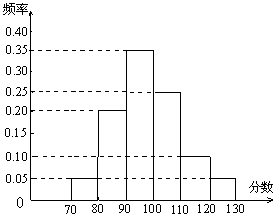
某校共有800名学生,高三一次月考之后,为了了解学生学习情况,用分层抽样方法从中抽出若干学生此次数学成绩,按成绩分组,制成如下的频率分布表:
| 组号 | 第 一 组 | 第 二 组 | 第 三 组 | 第 四 组 | 第 五 组 | 第 六 组 | 第 七 组 | 第 八 组 | 合计 |
| 分组 | 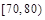 | 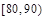 | 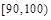 | 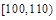 | 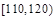 | 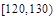 |  | 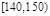 | |
| 频数 | 4 | 6 | 20 | 22 | 18 | 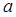 | 10 | 5 | 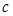 |
| 频率 | 0.04 | 0.06 | 0.20 | 0.22 | 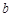 | 0.15 | 0.10 | 0.05 | 1 |
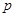 ;
;(Ⅱ) 为了了解数学成绩在120分以上的学生的心理状态,现决定在第六、七、八组中用分层抽样方法抽取6名学生的成绩,并在这6名学生中在随机抽取2名由心理老师张老师负责面谈,求第七组至少有一名学生与张老师面谈的概率;
(Ⅲ) 估计该校本次考试的数学平均分。
(本小题满分12分)某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的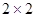 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为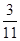 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.
附:
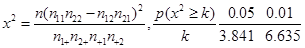 )
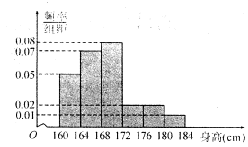
) 下表是关于某设备的使用年限(年)和所需要的维修费用y (万元)的几组统计数据:
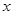 | 2 | 3 | 4 | 5 | 6 |
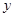 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(2)请根据散点图,判断y与x之间是否有较强线性相关性,若有求线性回归直线方程
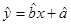 ;
;(3)估计使用年限为10年时,维修费用为多少?
(参考数值:
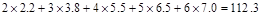 )
)参考公式:
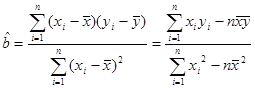 ;
;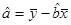 ;
; 
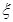 ,求
,求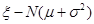 .则
.则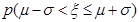 =0.6826,
=0.6826,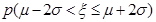 ="0.9544,"
="0.9544," 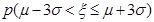 =0.9974.
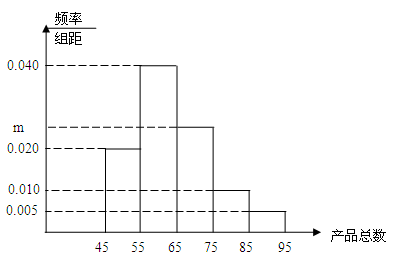
=0.9974. 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为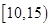 ,
,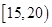 ,
,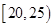 ,
,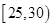 ,
,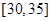 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在