题目内容
(本题满分12分)
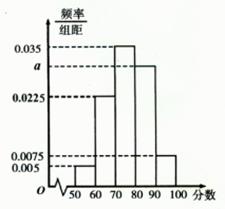
为调查某工厂工人生产某种产品的能力,随机抽查了一些工人某天生产产品的数量,产品数量的分组区间为[45,55), [55,65), [65,75), [75,85), [85,95),由此得到频率分布直方图如图所示,保存中不慎丢失一些数据,但已知第一组 ([45,55) ]有4人;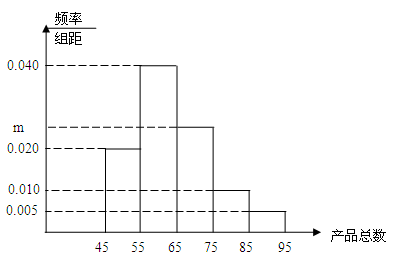
(Ⅰ)求被抽查的工人总人数n及图中所示m为多少;
(Ⅱ)求这些工人中一天生产该产品数量在[55,75)之间的人数是多少。
(Ⅰ)m=0.025, n="20" (Ⅱ)13人
解析试题分析:根据直方图分析可知该产品数量在[55,75)的频率,又由频率与频数的关系计算可得生产该产品数量在[55,75)的人数
(Ⅰ)m=0.025, n="20"
(Ⅱ)解:由直方图可知:生产该产品数量在[55,75)的频率=0.065×10,∴生产该产品数量在[55,75)的人数=20×(0.065×10)=13,故答案为13.
考点:直方图的运用
点评:解决该试题的关键是理解直方图中方形的面积代表频率,同时能根据频率与频数的关系式来得到求解,属于基础题。

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,
小数点后的一位数字为叶)如图示:
| | |
| 4 | 3 5 6 6 6 7 7 7 8 8 9 9 |
| 5 | 0 1 1 2 |
(2)若视力测试结果不低于5.0,则称为“健康视力”,求校医从这16人中随机选取3人,至多有1人是“健康视力”的概率;
(3)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记
 表示抽到“健康视力”学生的人数,求
表示抽到“健康视力”学生的人数,求 的分布列及数学期望
的分布列及数学期望 为了解目前老年人居家养老还是在敬老院养老的意向,共调查了50名老年人,其中男性明确表示去敬老院养老的有5人,女性明确表示居家养老的有10人,已知在全部50人中随机地抽取1人明确表示居家养老的概率为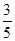 。
。
(1)请根据上述数据建立一个2×2列联表;
(2)居家养老是否与性别有关?请说明理由。
参考公式: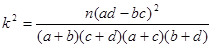
参考数据:
 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
以下是某地搜集到的新房屋的销售价格 和房屋的面积
和房屋的面积 的数据:
的数据:
房屋面积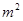 | 110 | 90 | 80 | 100 | 120 |
| 销售价格(万元) | 33 | 31 | 28 | 34 | 39 |
(2)求线性回归方程;
(3)据(2)的结果估计当房屋面积为
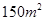 时的销售价格.
时的销售价格.(提示:
 ,
, 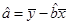 ,
,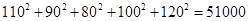 ,
,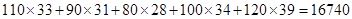 )
) (本题满分12分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
 | 文艺节目 | 新闻节目 | 总计 |
| 20~40岁 | 40 | 18 | 58 |
| 大于40岁 | 15 | 27 | 42 |
| 总计 | 55 | 45 | 100 |
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应抽取几名?
(本题满分12分)
某校为了探索一种新的教学模式,进行了一项课题实验,乙班为实验班,甲班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,成绩如下表(总分:150分):
甲班
| 成绩 | 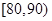 |  | 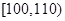 | 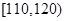 | 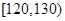 |
| 频数 | 4 | 20 | 15 | 10 | 1 |
| 成绩 | 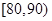 |  | 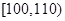 | 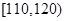 | 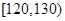 |
| 频数 | 1 | 11 | 23 | 13 | 2 |
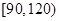 内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;(2)根据所给数据可估计在这次测试中,甲班的平均分是101.8,请你估计乙班的平均分,并计算两班平均分相差几分;
(3)完成下面2×2列联表,你认为在犯错误的概率不超过0.025的前提下, “这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由。
| | 成绩小于100分 | 成绩不小于100分 | 合计 |
| 甲班 | 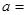 | 26 | 50 |
| 乙班 | 12 | 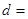 | 50 |
| 合计 | 36 | 64 | 100 |
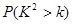 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(12分)在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
附: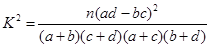 ;
;
 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 的值;
的值;