题目内容
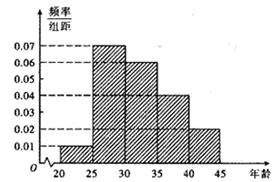
(11分)为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为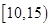 ,
,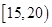 ,
,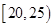 ,
,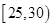 ,
,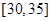 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在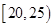 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工人不在同一组的概率是多少?
(Ⅰ)m=20(位)。(Ⅱ)选取这2人不在同组的概率为 。
。
解析试题分析:(Ⅰ)根据直方图可知产品件数在[20,25)内的人数为m×5×0.06=6, ……2分
则m=20(位)。 ……4分
(Ⅱ)根据直方图可知产品件数在[10,15),[15,20),组内的人数分别为2,4.设六人分别为x,y,a,b,c,d ……5分
Ω={(x,y),(x,a),(x,b),(x,c),(x,d),(y,a),(y,b),(y,c),(y,d),(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)}共15个基本事件 ……8分
设这2位工人不在同一组为A事件,其中包含(x,a),(x,b),(x,c),(x,d),(y,a),(y,b),(y,c),(y,d),
共8个, ……9分
则P(A)=  ……11分
……11分
答:选取这2人不在同组的概率为 。
。
考点:本题主要考查古典概型的概率计算,直方图。
点评:综合题,古典概型概率的计算,关键是明确基本事件总数及导致事件发生的基本事件数,直方图中小矩形面积=(频率/组距)×组距。

 阅读快车系列答案
阅读快车系列答案为了解目前老年人居家养老还是在敬老院养老的意向,共调查了50名老年人,其中男性明确表示去敬老院养老的有5人,女性明确表示居家养老的有10人,已知在全部50人中随机地抽取1人明确表示居家养老的概率为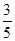 。
。
(1)请根据上述数据建立一个2×2列联表;
(2)居家养老是否与性别有关?请说明理由。
参考公式: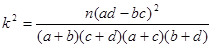
参考数据:
 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
一次考试中,五名学生的数学、物理成绩如下表所示:
| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学(x分 | 89 | 91 | 93 | 95 | 97 |
| 物理(y分) | 87 | 89 | 89 | 92 | 93 |
(1)请在图的直角坐标系中作出这些数据的散点图,并求出这些数据的同归方程;
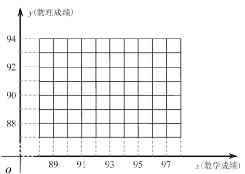
(2)要从4名数学成绩在90分以上的同学中选2人参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望E(X)的值.
(12分)在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
附: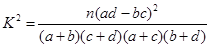 ;
;
 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(本小题满分12分)一个容量为M的样本数据,其频率分布表如下.
(Ⅰ)表中a= ,b = ;
(Ⅱ)画出频率分布直方图;
(Ⅲ)用频率分布直方图,求出总体的众数及平均数的估计值.
频率分布表
| 分组 | 频数 | 频率 | 频率/组距 |
| (10,20] | 2 | 0.10 | 0.010 |
| (20,30] | 3 | 0.15 | 0.015 |
| (30,40] | 4 | 0.20 | 0.020 |
| (40,50] | a | b | 0.025 |
| (50,60] | 4 | 0.20 | 0.020 |
| (60, 70] | 2 | 0.10 | 0.010 |
频率分布直方图

 ,
,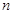 值,并补全频数条形图;
值,并补全频数条形图;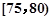 ,第2组
,第2组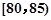 ,第3组
,第3组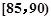 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.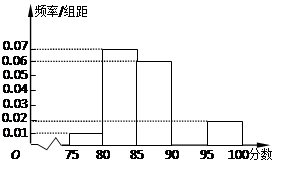
 男 女
男 女 15 7 7 8 9 9 9
15 7 7 8 9 9 9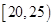 ,第2组
,第2组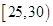 ,第3组
,第3组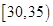 ,第4组
,第4组 ,第5组
,第5组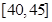 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.