题目内容
【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(I)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(II)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励. 现用样本估计总体,从上述5个销售单价中任选2个销售单价,求抽到的产品含有月销售量不低于10万件的概率.
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为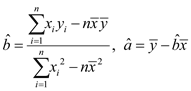 . 参考数据:
. 参考数据:![]() .
.
【答案】(I)![]() , 8.75元;(II)
, 8.75元;(II)![]() .
.
【解析】
(I) 求得![]() 、
、![]() 的平均数,根据公式求得
的平均数,根据公式求得![]() ,即可得回归方程,进而预测销售量不低于12万件时销售单价的最大值;
,即可得回归方程,进而预测销售量不低于12万件时销售单价的最大值;
(II) 根据古典概型概率,列出满足条件的组合,即可求得满足月销售量不低于10万件的概率。
(I)![]() ,
,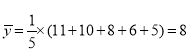
![]()
则![]()
所以![]() 关于
关于![]() 的回归直线方程为
的回归直线方程为![]()
要使月销售量不低于12万件,则有![]() ,解得
,解得![]()
所以销售单价的最大值为8.75元 .
(II)由题意可得,销售单价共有5个,其中使得月销售量不低于10万件的有2个记为![]() ,月销售量不低于8万件且不足10万件的有1个记为
,月销售量不低于8万件且不足10万件的有1个记为![]() ,月销售量低于8万件的有2个记为
,月销售量低于8万件的有2个记为![]() .从中抽2个其有10种,分别是
.从中抽2个其有10种,分别是![]()
![]()
![]() ,指定事件数有7种
,指定事件数有7种
所求概率![]() .
.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目