Question

【题目】如图，在三棱锥P﹣ABC中，PA=PC=5，PB=4，AB=BC=2 ，∠ACB=30°，PA=PC=5，PB=4，AB=BC=2 ，∠ACB=30°．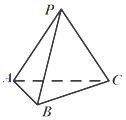

（1）求证：AC⊥PB；
（2）求三棱锥P﹣ABC的体积．

Answer 1

【答案】
（1）证明：取AC的中点D，连接PD、BD．

∵AB=BC，PA=AC，D为AC的中点，

∴PD⊥AC，BD⊥AC，

又BD平面PBD，PD平面PBD，BD∩PD=D，

∴AC⊥平面PBD．

∵PB平面PBD，

∴AC⊥PB

（2）解：VP﹣ABC=VP﹣ABD+VP﹣BCD=VA﹣PBD+VC﹣PBD

在△ABC中，AB=BC，∠ACB=30°，D是AC中点

∴ ，AD=DC=3在△PCD中，PD⊥DC，PC=5，DC=3，∴PD=4

∴ ，

VA﹣PBD= ×S△PBD×AD= × = ，

又 ，

∴

【解析】（1）取AC的中点D，连接PD、BD，利用三线合一得出PD⊥AC，BD⊥AC，于是AC⊥平面PBD，从而得出AC⊥PB；（2）计算AC，PD从而得出PB=PD，求出△PBD的面积，则VP﹣ABC= S△PBDAC．求解即可．
【考点精析】根据题目的已知条件，利用直线与平面垂直的性质的相关知识可以得到问题的答案，需要掌握垂直于同一个平面的两条直线平行．