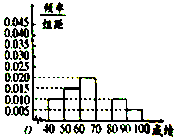题目内容
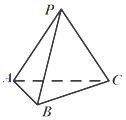
【题目】如图,三棱柱![]() 中,
中, ![]() .
.
(Ⅰ)证明: ![]() ;
;
(Ⅱ)平面![]()
![]() 平面
平面![]() ,
, ![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:
(1)利用题意首先证得![]() ,然后利用线面垂直的定义即可证得题中的结论;
,然后利用线面垂直的定义即可证得题中的结论;
(2)建立空间直角坐标系,结合平面的法向量和直线的方向向量可得直线![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() .
.
试题解析:
(1)证明:如图所示,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() .因为
.因为![]() ,
,
所以![]() .由于
.由于![]() ,
, ![]() ,
,
故![]() 为等边三角形,所以
为等边三角形,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
又![]() ,故
,故![]()
(2)由(1)知![]() ,
, ![]() ,又
,又![]() ,交线为
,交线为![]() ,
,
所以![]() ,故
,故![]() 两两相互垂直.
两两相互垂直.
以![]() 为坐标原点,
为坐标原点, ![]() 的方向为
的方向为![]() 轴的正方向,
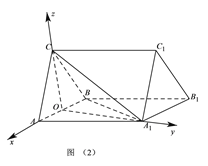
轴的正方向, ![]() 为单位长,建立如图(2)所示的空间直角坐标系
为单位长,建立如图(2)所示的空间直角坐标系![]() .由题设知
.由题设知![]() ,
,
则![]() ,
, ![]() ,
, ![]() .
.
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则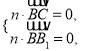 即
即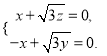 可取
可取![]() 故
故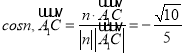 .
.
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()

 名校课堂系列答案
名校课堂系列答案【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网上叫外卖也开始成为不少人日常生活中不可或缺的一部分.为了解网络外卖在![]() 市的普及情况,
市的普及情况, ![]() 市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到表格:(单位:人)
市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到表格:(单位:人)
经常使用网络外卖 | 偶尔或不用网络外卖 | 合计 | |
男性 | 50 | 50 | 100 |
女性 | 60 | 40 | 100 |
合计 | 110 | 90 | 200 |
(1)根据表中数据,能否在犯错误的概率不超过![]() 的前提下认为
的前提下认为![]() 市使用网络外卖的情况与性别有关?
市使用网络外卖的情况与性别有关?
(2)①现从所抽取的女网民中利用分层抽样的方法再抽取5人,再从这5人中随机选出3人赠送外卖优惠券,求选出的3人中至少有2人经常使用网络外卖的概率;
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |