题目内容
【题目】已知函数f(x)=![]() ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
(1)证明:a>0;
(2)若z=a+2b,求z的取值范围.
【答案】见解析
【解析】
(1)证明 求函数f(x)的导数
f′(x)=ax2-2bx+2-b.
由函数f(x)在x=x1处取得极大值,
在x=x2处取得极小值,
知x1、x2是f′(x)=0的两个根,
所以f′(x)=a(x-x1)(x-x2).
当x<x1时,f(x)为增函数,f′(x)>0,
由x-x1<0,x-x2<0得a>0.
(2)解 在题设下,0<x1<1<x2<2等价于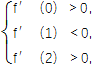
即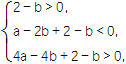 化简得
化简得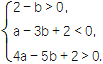
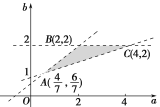
此不等式组表示的区域为平面aOb上的三条直线:
2-b=0,a-3b+2=0,4a-5b+2=0所围成的△ABC的内部,其三个顶点分别为A![]() ,B(2,2),C(4,2).
,B(2,2),C(4,2).
z在这三点的值依次为![]() ,6,8.
,6,8.
所以z的取值范围为![]() .
.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地
区调查了500位老年人,结果如下:
男 | 女 | |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否在犯错误的概率不超过0.01的前提下认为该地区的老年人需要志愿者提供帮助与性别有
关?
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
![]()