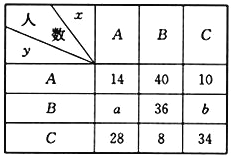
题目内容
【题目】已知函数f(x)=-x2+2ex+m-1,g(x)=x+![]() (x>0).
(x>0).
(1)若g(x)=m有实根,求m的取值范围;
(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.
【答案】见解析
【解析】
解 (1)∵x>0,∴g(x)=x+![]() ≥2
≥2![]() =2e,
=2e,
等号成立的条件是x=e.
故g(x)的值域是[2e,+∞),因而只需m≥2e,
则g(x)=m就有实根.故m∈[2e,+∞).
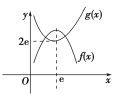
(2)若g(x)-f(x)=0有两个相异的实根,即g(x)=f(x)中函数g(x)与f(x)的图象有两个不同的交点,
作出g(x)=x+![]() (x>0)的大致图象.
(x>0)的大致图象.
∵f(x)=-x2+2ex+m-1=-(x-e)2+m-1+e2.
其对称轴为x=e,开口向下,最大值为m-1+e2.
故当m-1+e2>2e,即m>-e2+2e+1时,
g(x)与f(x)有两个交点,即g(x)-f(x)=0有两个相异实根.
∴m的取值范围是(-e2+2e+1,+∞).

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目