题目内容
已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)求以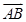 ,
,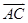 为边的平行四边形的面积;
为边的平行四边形的面积;
(2)若|a|=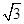 ,且a分别与
,且a分别与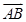 ,
,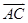 垂直,求向量a的坐标.
垂直,求向量a的坐标.
(1)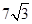 ;(2) a=(1,1,1),或a=(-1,-1,-1).
;(2) a=(1,1,1),或a=(-1,-1,-1).
解析试题分析:(1)由点的坐标可得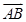 ,
,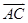 坐标,进而求得模长,及夹角余弦,可利用同角间基本关系式求得夹角正弦,以
坐标,进而求得模长,及夹角余弦,可利用同角间基本关系式求得夹角正弦,以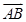 ,
,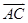 为边的平行四边形的面积,应该是以
为边的平行四边形的面积,应该是以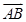 ,
,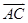 为边的三角形面积的二倍,利用三角形面积公式可求得;(2)设
为边的三角形面积的二倍,利用三角形面积公式可求得;(2)设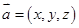 ,由两向量垂直坐标满足的关系式得关于
,由两向量垂直坐标满足的关系式得关于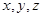 的方程组,解方程可得向量a的坐标.
的方程组,解方程可得向量a的坐标.
解:(1)由题意可得: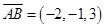 ,
,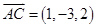 ,
,
∴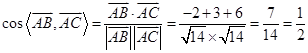 , 4分
, 4分
∴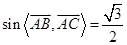 ,∴以
,∴以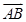 ,
,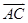 为边的平行四边形的面积为
为边的平行四边形的面积为 . 6分
. 6分
(2)设a=(x,y,z),
由题意得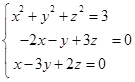 ,
,
解得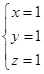 或
或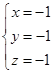 .
.
∴a=(1,1,1),或a=(-1,-1,-1) 12分
考点:空间向量的坐标运算,三角形面积公式.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
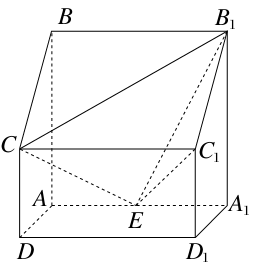
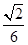 ,求线段AM的长.
,求线段AM的长. 的底面
的底面 是等腰直角三角形,
是等腰直角三角形, ,侧棱
,侧棱 底面
底面 ,
, 是
是 的中点,
的中点, 是
是 上的点.
上的点. 与
与 的大小(结果用反三角函数表示);
的大小(结果用反三角函数表示); ,求线段
,求线段 的长.
的长.
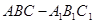 中,
中,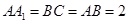 ,
,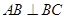 。M、N分别是AC和BB1的中点。
。M、N分别是AC和BB1的中点。 的大小。
的大小。 ⊥平面
⊥平面 ,
,  的长度。
的长度。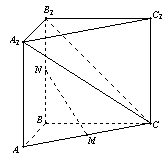
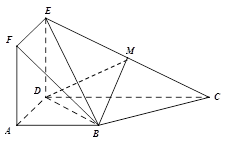
 与梯形
与梯形 所在的平面互相垂直,
所在的平面互相垂直,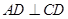 ,
, ∥
∥ ,
,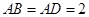 ,
,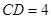 ,
,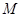 为
为 的中点.
的中点.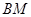 ∥平面
∥平面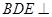 平面
平面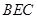 ;
;
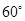 ,∠BAC
,∠BAC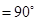 ,AD是BC上的高,沿AD把△ABD折起,使∠BDC
,AD是BC上的高,沿AD把△ABD折起,使∠BDC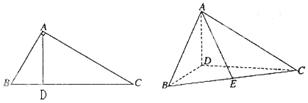
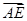 与
与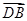 夹角的余弦值.
夹角的余弦值.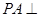 底面ABCD,
底面ABCD,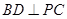 ,E是PA的中点.
,E是PA的中点.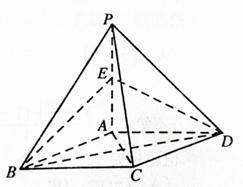
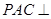 平面EBD;
平面EBD;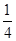 ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积.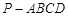 的底面为直角梯形,
的底面为直角梯形,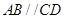 ,
,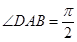 ,
,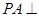 底面
底面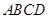 ,且
,且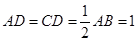 ,
,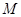 是
是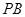 的中点.
的中点.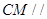 平面
平面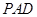 ;
; 与平面
与平面 所成的角为
所成的角为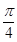 ,求二面角
,求二面角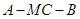 的余弦值.
的余弦值.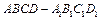 中,
中,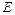 为
为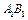 的中点,则异面直线
的中点,则异面直线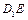 和
和 间的距离 .
间的距离 .