题目内容
【题目】设非空集合s={x|m≤x≤l}满足:当x∈S时,有y=x2∈S.给出如下三个命题:
①若m=1,则S={1};
②若m=﹣ ![]() ,则
,则 ![]() ≤l≤1;
≤l≤1;
③若l= ![]() ,则﹣
,则﹣ ![]() ≤m≤0.
≤m≤0.
④若l=1,则﹣1≤m≤0或m=1.
其中正确命题的是 .
【答案】①②③④
【解析】解:由定义设非空集合S={x|m≤x≤l}满足:当x∈S时,有y=x2∈S可知:符合定义的参数m的值一定大于等于﹣1,符合条件的l的值一定大于等于0,小于等于1,
如此才能保证l∈S时,有l2∈S即l2≤l,再对各个命题进行判断:
对于①m=1,m2=1∈S故必有 ![]() ,可得l=1,S={1},故正确;
,可得l=1,S={1},故正确;
②m=﹣ ![]() ,
, ![]() 则
则 ![]() ,解得
,解得 ![]() ≤l≤1,故正确;
≤l≤1,故正确;
③若l= ![]() ,则
,则 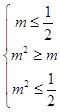 ,可解得﹣
,可解得﹣ ![]() ≤m≤0,故正确;
≤m≤0,故正确;
④若l=1,则 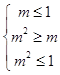 可解得﹣1≤m≤0或m=1,故正确.
可解得﹣1≤m≤0或m=1,故正确.
所以答案是:①②③④
【考点精析】通过灵活运用命题的真假判断与应用,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系即可以解答此题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目