Question

【题目】为了估计某校的一次数学考试情况，现从该校参加考试的600名学生中随机抽出60名学生，其成绩（百分制）均在[40，100）上，将这些成绩分成六段[40，50），[50，60）…[90，100），后得到如图所示部分频率分布直方图．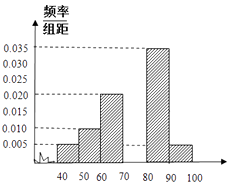

（1）求抽出的60名学生中分数在[70，80）内的人数；
（2）若规定成绩不小于85分为优秀，则根据频率分布直方图，估计该校优秀人数．
（3）根据频率分布直方图算出样本数据的中位数．

Answer 1

【答案】
（1）解：在频率分直方图中，小矩形的面积等于这一组的频率，频率的和等于1，

成绩在[70，80）内的频率1﹣（0.005+0.01+0.02+0.035+0.005）×10=0.25．

人数为0.25×60=15人

（2）解：估计该校的优秀人数为不小于85分的频率再乘以样本总量600，即

600×（ +0.005）×10=135人

（3）解：分数在[70，80）内的频率为0.25，

∵分数在[40，70）内的频率为：（0.005+0.010+0.020）×10=0.35＜0.5，

∴中位数在（70，80]内，

∵中位数要平分直方图的面积，

∴中位数为：70+ =76

【解析】（1）根据频率的和等于1求出成绩在[70，80）内的频率，计算对应的频数即可；（2）计算不小于85分的频数即可；（3）根据中位数平分频率分布直方图的面积，求出即可．
【考点精析】本题主要考查了频率分布直方图和平均数、中位数、众数的相关知识点，需要掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息；⑴平均数、众数和中位数都是描述一组数据集中趋势的量；⑵平均数、众数和中位数都有单位；⑶平均数反映一组数据的平均水平，与这组数据中的每个数都有关系，所以最为重要，应用最广；⑷中位数不受个别偏大或偏小数据的影响；⑸众数与各组数据出现的频数有关，不受个别数据的影响，有时是我们最为关心的数据才能正确解答此题．