Question

5．已知球O的半径OP的长为1，O₁是OP的中点，过O₁作平面垂直于直线OP，交球面于小圆⊙O₁，若A、B是小圆⊙O₁圆弧上两点，且A、B之间的球面距离为$\frac{π}{3}$，则∠AO₁B的大小为2arcsin$\frac{\sqrt{3}}{3}$（结果用反三角函数值表示）．

Answer 1

分析 画出图形，通过A、B之间的球面距离为$\frac{π}{3}$，球的半径为1，求解△AO₁B的边长，然后求解所求角．

解答 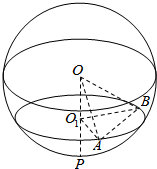解：如图：球O的半径OP的长为1，O₁是OP的中点，过O₁作平面垂直于直线OP，交球面于小圆⊙O₁，若A、B是小圆⊙O₁圆弧上两点，且A、B之间的球面距离为$\frac{π}{3}$，
可得：OA=0B=1，∠AOB=$\frac{π}{3}$，OO₁=$\frac{1}{2}$，则AO₁=BO₁=$\frac{\sqrt{3}}{2}$，AB=1．
sin$（\frac{1}{2}{∠AO}_{1}B）$=$\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}$=$\frac{\sqrt{3}}{3}$，
∴$\frac{1}{2}{∠AO}_{1}B$=arcsin$\frac{\sqrt{3}}{3}$．
∠AO₁B的大小为：2arcsin$\frac{\sqrt{3}}{3}$．
故答案为：2arcsin$\frac{\sqrt{3}}{3}$．

点评 本题考查球面距离以及相关计算，考查空间想象能力以及计算能力．