题目内容
2.已知函数y=f(x)的图象如图所示,则其导函数y=f′(x)的图象可能是( )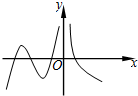
| A. |  | B. | 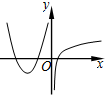 | C. | 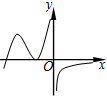 | D. | 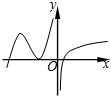 |
分析 观察函数y=f(x)的图象知,f(x)在(0,+∞)上是减函数,f(x)在(-∞,0)从左到右,先增再减最后增;从而确定导数的正负,从而求解.
解答 解:观察函数y=f(x)的图象知,
f(x)在(0,+∞)上是减函数,故y=f′(x)<0在(0,+∞)恒成立,故排除B,D,
f(x)在(-∞,0)从左到右,先增再减最后增,故y=f′(x)在(-∞,0)从左到右,先“+”再“-”最后“+”恒成立,故排除C,
故选:A.
点评 本题考查了导数的综合应用,同时考查了数形结合的思想应用,属于基础题

练习册系列答案
相关题目
13.已知实数a<b,x<y,且(x-a)(x-b)<0,(y-a)(y-b)>0,则下列关系式正确的是( )
| A. | a<x<y<b | B. | a<x<b<y | C. | x<a<y<b | D. | x<y<a<b |
17.设f(x)=$\left\{\begin{array}{l}{4{e}^{x-2}(x<3)}\\{lo{g}_{5}(3x+1)(x≥3)}\end{array}\right.$,则f[f(ln2+2)]=( )
| A. | log515 | B. | 2 | C. | 5 | D. | log5(3e2+1) |
7.直线l:y=kx+1与圆x2+y2=1相交于A,B两点,则“△OAB的面积为$\frac{{\sqrt{3}}}{4}$”是“k=$\sqrt{3}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.设数列{an}满足an+1+an-1≤2an(n∈N*,n≥2),则称数列{an}为凸数列,已知等差数列{bn}的公差为lnd,首项b1=2,且数列{$\frac{{b}_{n}}{n}$}为凸数列,则d的取值范围是( )
| A. | (0,e2] | B. | [e2,+∞) | C. | (2,e2] | D. | [2,+∞) |
11.函数f(x)=x3-3x-1,x∈[-3,2].则f(x)的最大值与最小值的差为( )
| A. | 20 | B. | 18 | C. | 4 | D. | 0 |