题目内容

1．在平面直角坐标系xOy中，直线2x-y-4=0与直线y=x-1的交点为M，过点A（0，3）作直线l，使得点M到直线l的距离为1．求直线l的方程．

分析 首先通过两直线方程求出交点M的坐标，然后利用点到直线的距离公式得到关于斜率k的等式求直线斜率．

解答 解：由$\left\{\begin{array}{l}2x-y-4=0\\ y=x-1\end{array}\right.$解得点M（3，2），…（3分）
由题意可知，直线l的斜率必存在．
由于直线l过点A（0，3），故可设直线l的方程为y=kx+3．…（6分）
由题意，$\frac{{|{3k+1}|}}{{\sqrt{{k^2}+1}}}=1$，解得$k=0或-\frac{3}{4}$，…..（10分）
故所求直线方程为y=3或3x+4y-12=0．…．（12分）

点评 本题考查了点到直线的距离公式的运用；属于基础题．

练习册系列答案
相关题目
11．已知椭圆$\frac{y^2}{a^2}$+$\frac{x^2}{b^2}$=1（a＞b＞0）经过点P（${\frac{{\sqrt{6}}}{2}$，$\frac{1}{2}}$），离心率为$\frac{{\sqrt{2}}}{2}$，动点 M（2，t）（t＞0）．
（1）求椭圆的标准方程；
（2）求以 O M（ O为坐标原点）为直径且被直线3x-4y-5=0截得的弦长为2的圆的方程；
（3）设F是椭圆的右焦点，过点F作 O M的垂线与以 O M为直径的圆交于点 N，证明线段 O N的长为定值，并求出这个定值．
12．已知f（x）=$\left\{\begin{array}{l}{2^x}+3，x≤0\\{（x-2）^2}，x＞0\end{array}$在区间（m2-4m，2m-2）上能取得最大值，则实数m的取值范围为（1，3]．
9．若x∈（1，+∞），则y=x+$\frac{2}{x-1}$的最小值是2$\sqrt{2}$+1．
16．若直线a不平行于平面α，则下列结论成立的是（　　）
A．α内所有的直线都与a异面B．α内不存在与a平行的直线
C．α内所有的直线都与a相交D．直线a与平面α有公共点
6．已知向量$\overrightarrow{m}$=（x-1，1），$\overrightarrow{n}$=（1，y），若$\overrightarrow{m}⊥\overrightarrow{n}$，则2x+2y的最小值为（　　）
A．2B．4C．2$\sqrt{2}$D．4$\sqrt{2}$
13．设x，y满足约束条件$\left\{\begin{array}{l}{3x-y-6≤0}\\{x-y+2≥0}\\{x≥0，y≥0}\end{array}\right.$，则目标函数z=x+y最大值与最小值的和为10．
10．已知集合A={x|（x-a+1）（x-1）＜0}，B={x|log2x≤1}
（1）求B；
（2）若A∩B=A，求实数a的取值范围．
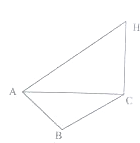11．某中学高二研究性学校小组按以下方案测算一种烟花的垂直发射高度：A、B、C三地位于同一水平面上，在C处进行该烟花的垂直发射，观测点A、B两地相距100米，∠BAC=60°，在A地听到地面C处发射声音的时间比B地晚$\frac{2}{17}$秒，在A地测得这种烟花至高点H时的仰角为30°，求这种烟花的垂直发射高度（声音的传播速度为340米/秒）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网