题目内容
12.已知f(x)=$\left\{\begin{array}{l}{2^x}+3,x≤0\\{(x-2)^2},x>0\end{array}$在区间(m2-4m,2m-2)上能取得最大值,则实数m的取值范围为(1,3].分析 作函数f(x)=$\left\{\begin{array}{l}{2^x}+3,x≤0\\{(x-2)^2},x>0\end{array}$的图象,结合图象及指数函数与二次函数的性质可得$\left\{\begin{array}{l}{{m}^{2}-4m<0}\\{0<2m-2≤4}\end{array}\right.$,从而解得.
解答 解:作函数f(x)=$\left\{\begin{array}{l}{2^x}+3,x≤0\\{(x-2)^2},x>0\end{array}$的图象如下,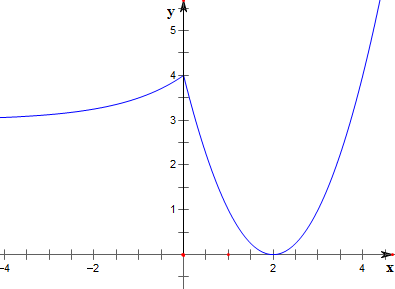
结合图象可知,
$\left\{\begin{array}{l}{{m}^{2}-4m<0}\\{0<2m-2≤4}\end{array}\right.$;
解得,1<m≤3;
故实数m的取值范围为(1,3];
故答案为:(1,3].
点评 本题考查了基本初等函数的图象的作法及数形结合的应用,同时考查了函数的最值,属于中档题.

练习册系列答案
相关题目
3.与双曲线C:$\frac{{x}^{2}}{12}-\frac{{y}^{2}}{4}$=1共焦点,且过点(0,3)的椭圆的离心率为( )
| A. | $\frac{2\sqrt{34}}{17}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{4\sqrt{7}}{7}$ | D. | $\frac{4}{5}$ |
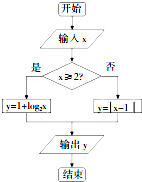 如图程序框图,当输出的任何一个确定的y值时恰好只对应输入唯一的x值,则这是输出的y值的范围是[0,+∞).
如图程序框图,当输出的任何一个确定的y值时恰好只对应输入唯一的x值,则这是输出的y值的范围是[0,+∞).