题目内容
【题目】已知二次函数![]() 同时满足:①在定义域内存在
同时满足:①在定义域内存在![]() ,使得
,使得![]() 成立;
成立;
②不等式![]() 的解集有且只有一个元素;数列
的解集有且只有一个元素;数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() ,
,![]() 。
。
(Ⅰ)求![]() 的表达式;
的表达式;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)设![]() ,
,![]() ,
,![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() 对任意
对任意![]() ,且
,且![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】试题分析: (1) 由①②可知,函数f(x)的![]() ,且对称轴大于0.由
,且对称轴大于0.由![]() 或
或![]() 分类讨论可解.(2)由(1)得
分类讨论可解.(2)由(1)得![]() ,根据数列通项与和的关系
,根据数列通项与和的关系![]() ,
,![]() 可求得
可求得![]() .(3)
.(3)![]() , 当
, 当![]() 时,
时,![]() ,由分组求和得
,由分组求和得![]() …
…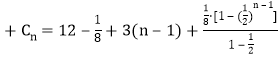
![]() ,代入,分离参数得
,代入,分离参数得![]() ,当n=2时取最小值9,所以
,当n=2时取最小值9,所以![]() .
.
试题解析:(1)由不等式![]() 的解集有且只有一个元素,得:
的解集有且只有一个元素,得:![]()
![]() 或
或![]()
当![]() 时,
时,![]() ,在
,在![]() 上单增,不合题意,舍
上单增,不合题意,舍
当![]() 时,
时,![]() 在
在![]() 上单减,
上单减,
故存在![]() ,使得
,使得![]() 成立
成立 ![]()
(2)由①知:![]() 当
当![]() 时,
时,![]()
当![]() 时,
时,![]()
![]()
![]()
(3)![]()
![]()
当![]() 时,
时,![]()
![]() …
…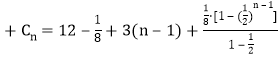
![]()
![]() 对
对![]() 恒成立
恒成立
![]()
设![]()
![]() ,是关于
,是关于![]() 的增函数
的增函数
![]()
![]() 的取值范围是:
的取值范围是:![]()

练习册系列答案
相关题目

