题目内容
【题目】如图所示,正三棱柱![]() 的高为2,
的高为2,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点
的中点
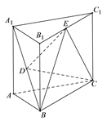
(1)证明:![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积为
的体积为![]() ,求该正三棱柱的底面边长.
,求该正三棱柱的底面边长.
【答案】(1)见解析(2)2
【解析】
试题分析:(1)由三角形中位线性质得DE//AC1,再根据线面平行判定定理得结果(2)根据平行性质得D到平面BCC1B1的距离是A到平面BCC1B1的距离的一半,再根据锥体体积公式列方程解得底面边长
试题解析:(Ⅰ)证明:如图,连接AB1,AC1,
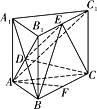
易知D是AB1的中点,
又E是B1C1的中点,
所以在![]() 中,DE//AC1,
中,DE//AC1,
又DE![]() 平面ACC1A1,AC1
平面ACC1A1,AC1![]() 平面ACC1A1,
平面ACC1A1,
所以DE//平面ACC1A1.
(Ⅱ)解:![]() ,
,
![]() D是AB1的中点,
D是AB1的中点,
![]() D到平面BCC1B1的距离是A到平面BCC1B1的距离的一半,
D到平面BCC1B1的距离是A到平面BCC1B1的距离的一半,
如图,作AF![]() BC交BC于F,由正三棱柱的性质,易证AF
BC交BC于F,由正三棱柱的性质,易证AF![]() 平面BCC1B1,
平面BCC1B1,
设底面正三角形边长为![]() ,则三棱锥DEBC的高h=
,则三棱锥DEBC的高h=![]() AF=
AF=![]() ,
,
![]() ,所以
,所以![]() ,
,
解得![]() .
.
所以该正三棱柱的底面边长为2.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目