题目内容
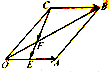 如图,在平行四边形OABC中,E是OA的中点,F在对角线OB上,且OF=
如图,在平行四边形OABC中,E是OA的中点,F在对角线OB上,且OF=| 1 |
| 3 |
| OA |
| a |
| OC |
| b |
(1)试用
| a |
| b |
| CE |
| CF |
(2)证明:C,E,F三点共线.
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:(1)根据向量的减法及共线向量基本定理即可用
,
表示出
,
;
(2)根据(1)求得的
,
即可找到一个实数k,使得
=k
,从而得出C,E,F三点共线.
| a |
| b |
| CE |
| CF |
(2)根据(1)求得的
| CE |
| CF |
| CE |
| CF |
解答:
解:(1)根据已知条件有:
=
-
=
-
=
-
;
=
-
=
-
=
(
+
)-
=
-
;
(2)证明:由(1)知
=
;
∴
,
共线;
∴C,E,F三点共线.
| CE |
| OE |
| OC |
| 1 |
| 2 |
| OA |
| OC |
| 1 |
| 2 |
| a |
| b |
| CF |
| OF |
| OC |
| 1 |
| 3 |
| OB |
| OC |
| 1 |
| 3 |
| a |
| b |
| b |
| 1 |
| 3 |
| a |
| 2 |
| 3 |
| b |
(2)证明:由(1)知
| CE |
| 3 |
| 2 |
| CF |
∴
| CE |
| CF |
∴C,E,F三点共线.
点评:考查向量的减法,向量的平行四边形法则,以及共线向量基本定理,向量共线与点共线的关系.

练习册系列答案
相关题目
已知双曲线
-
=1的一条渐近线方程为y=
x,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
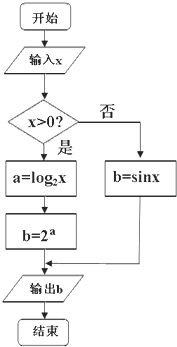 如图所示的程序框图,若两次输入的x值分别是3π和-
如图所示的程序框图,若两次输入的x值分别是3π和-| π |
| 3 |
A、1,
| ||||
B、0,
| ||||
C、-π,-
| ||||
D、3π,-
|
在△ABC中,角A,B,C的对边长分别为a,b,c,a=8,B=60°,C=75°,则b=( )
A、4
| ||
B、4
| ||
C、4
| ||
D、
|