题目内容
已知椭圆
+
=1(a>b>0)的左右焦点分别为F1、F2,离心率e=
,直线y=x+4经过椭圆的左焦点F1.
(1)求该椭圆的方程;
(2)若该椭圆上有一点P满足:
•
=0,求△F1PF2的面积.
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 5 |
(1)求该椭圆的方程;
(2)若该椭圆上有一点P满足:
| PF1 |
| PF2 |
考点:椭圆的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)求出焦点的坐标,运用离心率公式和a,b,c的关系,即可得到椭圆方程;
(2)运用勾股定理,结合椭圆的定义,求得|PF1|•|PF2|=18,再由三角形面积公式即可得到.
(2)运用勾股定理,结合椭圆的定义,求得|PF1|•|PF2|=18,再由三角形面积公式即可得到.
解答:
解:(1)直线y=x+4与x轴的交点的坐标为(-4,0),
则F1的坐标为(-4,0),c=4.
∵e=
=
,∴a=5,b2=a2-c2=9.
则椭圆的方程为
+
=1;
(2)由
•
=0得:
⊥
,所以PF1⊥PF2,
所以△PF1F2是直角三角形,
|PF1|2+|PF2|2=|F1F2|2=64.
又∵|PF1|+|PF2|=2a=10,
∴|PF1|2+|PF2|2+2|PF1|•|PF2|=100,
则|PF1|•|PF2|=18
故S△F1PF2=
|PF1|•|PF2|=9.
则F1的坐标为(-4,0),c=4.
∵e=
| c |
| a |
| 4 |
| 5 |
则椭圆的方程为
| x2 |
| 25 |
| y2 |
| 9 |
(2)由
| PF1 |
| PF2 |
| PF1 |
| PF2 |
所以△PF1F2是直角三角形,
|PF1|2+|PF2|2=|F1F2|2=64.
又∵|PF1|+|PF2|=2a=10,
∴|PF1|2+|PF2|2+2|PF1|•|PF2|=100,
则|PF1|•|PF2|=18
故S△F1PF2=
| 1 |
| 2 |
点评:本题考查椭圆的定义、方程和性质:离心率,考查平面向量的数量积的性质,考查三角形的面积公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
在平面直角坐标系中,不等式组
,(a是常数)表示的平面区域面积是9,那么实数a的值为( )
|
A、3
| ||
B、-3
| ||
| C、-5 | ||
| D、1 |
已知向量
=(1,k),
=(k-1,2),若
∥
,则正实数k的值为( )
| a |
| b |
| a |
| b |
| A、2 | B、1 |
| C、1或-2 | D、-1或2 |
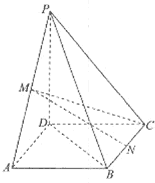 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,M、N分别为PA、BC的中点,且PD=AD=1,
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,M、N分别为PA、BC的中点,且PD=AD=1,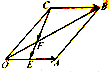 如图,在平行四边形OABC中,E是OA的中点,F在对角线OB上,且OF=
如图,在平行四边形OABC中,E是OA的中点,F在对角线OB上,且OF=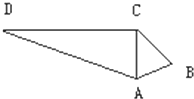 如图在四边形ABCD中,AC⊥DC,△ADC的面积为30cm2,DC=12cm,AB=3cm,BC=4cm求△ABC的面积.
如图在四边形ABCD中,AC⊥DC,△ADC的面积为30cm2,DC=12cm,AB=3cm,BC=4cm求△ABC的面积.