题目内容

已知复数z1=1+3i，z2=
3
cosα+isinα，求复数z=z1•z2实部的最值．
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：把z1=1+3i，z2=
3
cosα+isinα代入z=z1•z2，化简后得到z的实部，然后利用三角运算求实部的最值．
解答： 解：∵z1=1+3i，z2=
3
cosα+isinα，
∴z=z1•z2=（1+3i）（
3
cosα+isinα）
=
3
cosα+isinα+3
3
icosα-3sinα
=（
3
cosα-3sinα）+i（sinα+3
3
cosα），
∴z的实部为t=
3
cosα-3sinα=2
3
sin(
π
6
-α)．
∴当α=2kπ-
π
3
，k∈Z时，tmax=2
3
；
当α=2kπ-
4π
3
，k∈Z时，tmin=-2
3
．
点评：本题考查了复数代数形式的乘除运算，考查了三角函数值域的求法，是基础题．
练习册系列答案
相关题目
坐标平面上的点（x，y）位于线性约束条件
x+y≤5
y≤x+1
x≥0
y≥0
所表示的区域内（含边界），则目标函数z=3x+4y的最大值是
 
．
在平面直角坐标系中，不等式组
x+y≥0
x-y+4≥0
x≤a
，（a是常数）表示的平面区域面积是9，那么实数a的值为（　　）
A、3
2
+2
B、-3
2
+2
C、-5
D、1
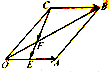如图，在平行四边形OABC中，E是OA的中点，F在对角线OB上，且OF=
1
3
OB，记
OA
=
a
，
OC
=
b
．
（1）试用
a
，
b
表示
CE
，
CF
；
（2）证明：C，E，F三点共线．
已知函数f（x）=xe-x（x∈R）
（Ⅰ）求函数f（x）的单调区间及极值；
（Ⅱ）求证：当x＞1时，f（x）＞f（2-x）；
（Ⅲ）如果x1≠x2，且f（x1）=f（x2），求证：x1+x2＞2．
已知△ABC的三个顶点在以O为球心的球面上，且∠B=90°，BC=1，AC=3，已知三棱锥O-ABC的体积为
14
6
，则球O的表面积为
 
．
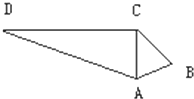如图在四边形ABCD中，AC⊥DC，△ADC的面积为30cm2，DC=12cm，AB=3cm，BC=4cm求△ABC的面积．
下列函数中，函数y=（
1
2
）x的反函数是（　　）
A、y=x 
1
2
B、y=2x
C、f（x）=log2x
D、y=log 
1
2
x
已知a，b是实数，则“a＞2且b＞2”是“a+b＞4且ab＞4”的（　　）
A、必要不充分条件
B、充分不必要条件
C、充要条件
D、既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网