题目内容
(满分12分)设函数 。
。
(Ⅰ)若在定义域内存在 ,而使得不等式
,而使得不等式 能成立,求实数
能成立,求实数 的最小值;
的最小值;
(Ⅱ)若函数 在区间
在区间 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 的取值范围。
的取值范围。
 。
。(Ⅰ)若在定义域内存在
 ,而使得不等式
,而使得不等式 能成立,求实数
能成立,求实数 的最小值;
的最小值;(Ⅱ)若函数
 在区间
在区间 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 的取值范围。
的取值范围。(Ⅰ)实数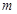 的最小值为
的最小值为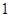 。(Ⅱ)
。(Ⅱ)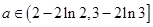 。
。
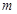 的最小值为
的最小值为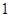 。(Ⅱ)
。(Ⅱ)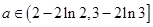 。
。试题分析:(Ⅰ)要使得不等式
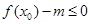 能成立,只需
能成立,只需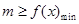 。
。 求导得:
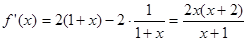 , ………3分
, ………3分∵函数
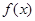 的定义域为
的定义域为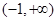 ,
,当
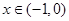 时,
时,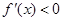 ,∴函数
,∴函数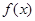 在区间
在区间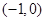 上是减函数;
上是减函数; 当
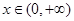 时,
时,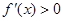 ,∴函数
,∴函数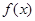 在区间(0,+∞)上是增函数。
在区间(0,+∞)上是增函数。 ∴
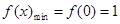 , ∴
, ∴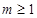 。故实数
。故实数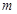 的最小值为
的最小值为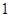 。 ………6分
。 ………6分(Ⅱ)由
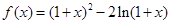 得:
得: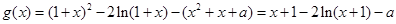
由题设可得:方程
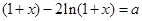 在区间
在区间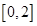 上恰有两个相异实根………8分
上恰有两个相异实根………8分 设
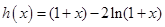 。∵
。∵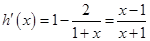 ,列表如下:
,列表如下: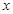 | 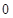 | 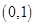 | 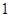 | 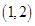 | 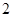 |
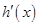 | | - | 0 | + | |
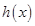 | 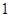 | 减函数 | 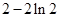 | 增函数 | 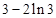 |
∵
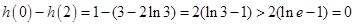 ,
,∴
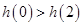 。
。从而有
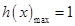 ,
,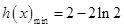 ………10分
………10分画出函数
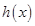 在区间
在区间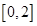 上的草图
上的草图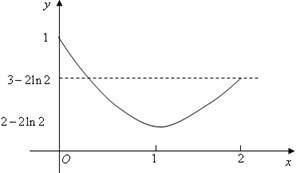
易知要使方程
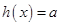 在区间
在区间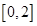 上恰有两个相异实根,
上恰有两个相异实根,只需:
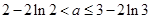 ,即:
,即: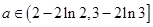 。 ………12分
。 ………12分点评:利用导数研究函数单调性、确定函数最值、研究函数图象,是导数的基本应用。本题将“恒成立”问题转化成求函数最值问题,将函数零点问题,转化成研究函数单调性、求最值问题,凸显转化与化归数学的重要性。

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
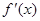 为f(x)的导函数,求证:
为f(x)的导函数,求证: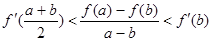
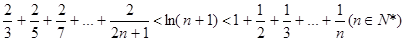
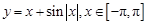 的大致图象是( )
的大致图象是( )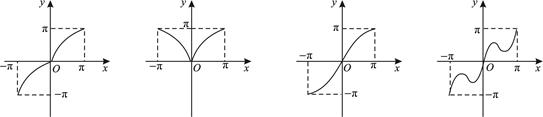
 在
在 处有极值,其图象在
处有极值,其图象在 处的切线与直线
处的切线与直线 平行.
平行. 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 ,
, ,
,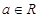 .
.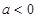 时,若函数
时,若函数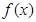 在区间
在区间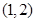 上是单调增函数,试求
上是单调增函数,试求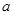 的取值范围;
的取值范围;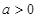 时,直接写出(不需给出演算步骤)函数
时,直接写出(不需给出演算步骤)函数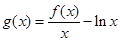 (
(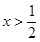 )的单调增区间;
)的单调增区间; ,使函数
,使函数 ,
,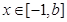 (
(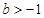 )在
)在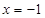 处取得最小值,试求实数
处取得最小值,试求实数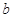 的最大值.
的最大值. ,
,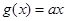 ,
,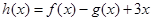 ,其中
,其中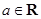 且
且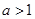 .
.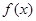 的导函数
的导函数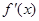 的最小值;
的最小值;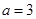 时,求函数
时,求函数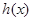 的单调区间及极值;
的单调区间及极值;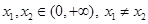 ,函数
,函数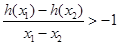 ,求实数
,求实数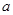 的取值范围.
的取值范围. 的导函数
的导函数 的图象大致是( )
的图象大致是( )
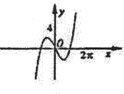



 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围; 时,求
时,求 上的最大值和最小值;
上的最大值和最小值; ,
, 恒成立.
恒成立.