题目内容
(本题满分12分)已知 在
在 处有极值,其图象在
处有极值,其图象在 处的切线与直线
处的切线与直线 平行.
平行.
(1)求函数的单调区间;
(2)若 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
 在
在 处有极值,其图象在
处有极值,其图象在 处的切线与直线
处的切线与直线 平行.
平行.(1)求函数的单调区间;
(2)若
 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。(1)当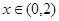 时,函数单调递减;当
时,函数单调递减;当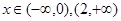 时,函数单调递增。
时,函数单调递增。
(2){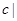
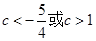 }。
}。
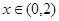 时,函数单调递减;当
时,函数单调递减;当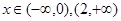 时,函数单调递增。
时,函数单调递增。(2){
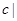
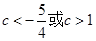 }。
}。试题分析:(1)由题意:
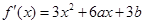 直线
直线 的斜率为
的斜率为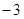 ;
;由已知
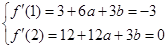 所以
所以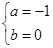 -----------------3分
-----------------3分所以由
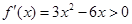 得心
得心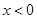 或
或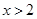 ;
;所以当
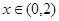 时,函数单调递减;
时,函数单调递减;当
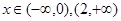 时,函数单调递增。-----------------6分
时,函数单调递增。-----------------6分(2)由(1)知,函数在
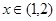 时单调递减,在
时单调递减,在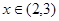 时单调递增;
时单调递增;所以函数在区间
 有最小值
有最小值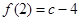 要使
要使 恒成立
恒成立只需
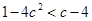 恒成立,所以
恒成立,所以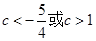 。
。故
 的取值范围是{
的取值范围是{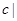
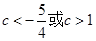 } -----------------12分
} -----------------12分点评:典型题,本题属于导数应用中的基本问题,像“
 恒成立”这类问题,往往要转化成求函数的最值问题,然后解不等式。
恒成立”这类问题,往往要转化成求函数的最值问题,然后解不等式。
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
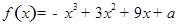 在区间[-2,2]的最大值为20,求它在该区间的最小值。
在区间[-2,2]的最大值为20,求它在该区间的最小值。
 ,求
,求 的单调区间;
的单调区间; ≥0时
≥0时 的取值范围.
的取值范围.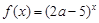 是R上的减函数;命题q:在
是R上的减函数;命题q:在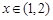 时,不等式
时,不等式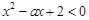 恒成立,若p∪q是真命题,求实数a的取值范围.
恒成立,若p∪q是真命题,求实数a的取值范围.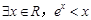 ”的否定是( )
”的否定是( )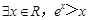
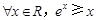
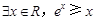
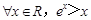
 。
。 ,而使得不等式
,而使得不等式 能成立,求实数
能成立,求实数 的最小值;
的最小值; 在区间
在区间 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 的取值范围。
的取值范围。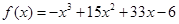 的单调增区间为 .
的单调增区间为 . .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.